§7. Примеры решения типовых задач. B2I что это

Как открыть B2I файлы - Файлы с расширением B2I

Что обозначает расширение B2I?

автор: Jay Geater, главный писатель по вопросам технологий

Вам кто-то послал по электронной почте файл B2I, и вы не знаете, как его открыть? Может быть, вы нашли файл B2I на вашем компьютере и вас заинтересовало, что это за файл? Windows может сказать вам, что вы не можете открыть его, или, в худшем случае, вы можете столкнуться с соответствующим сообщением об ошибке, связанным с файлом B2I.

До того, как вы сможете открыть файл B2I, вам необходимо выяснить, к какому виду файла относится расширения файла B2I.

Tip: Incorrect B2I file association errors can be a symptom of other underlying issues within your Windows operating system. These invalid entries can also produce associated symptoms such as slow Windows startups, computer freezes, and other PC performance issues. Therefore, it highly recommended that you scan your Windows registry for invalid file associations and other issues related to a fragmented registry.

Ответ:

Файлы B2I имеют Uncommon Files, который преимущественно ассоциирован с Binary Data.

Иные типы файлов также могут использовать расширение файла B2I. Если вам известны любые другие форматы файлов, использующие расширение файла B2I, пожалуйста, свяжитесь с нами, чтобы мы смогли соответствующим образом обновить нашу информацию.

Как открыть ваш файл B2I:

Самый быстрый и легкий способ открыть свой файл B2I — это два раза щелкнуть по нему мышью. В данном случае система Windows сама выберет необходимую программу для открытия вашего файла B2I.

В случае, если ваш файл B2I не открывается, весьма вероятно, что на вашем ПК не установлена необходимая прикладная программа для просмотра или редактирования файлов с расширениями B2I.

Если ваш ПК открывает файл B2I, но в неверной программе, вам потребуется изменить настройки ассоциации файлов в вашем реестре Windows. Другими словами, Windows ассоциирует расширения файлов B2I с неверной программой.

We highly recommend scanning your Windows registry for invalid file associations and other related registry issues.

Загрузки программного обеспечения, связанные с расширением файла B2I:

* Некоторые форматы расширений файлов B2I можно открыть только в двоичном формате.

Скачать FileViewPro для открытия ваших файлов B2I прямо сейчас

Установить необязательные продукты - FileViewPro (Solvusoft) | Лицензия | Политика защиты личных сведений | Условия | Удаление

B2I Инструмент анализа файлов™

Вы не уверены, какой тип у файла B2I? Хотите получить точную информацию о файле, его создателе и как его можно открыть?

Теперь можно мгновенно получить всю необходимую информацию о файле B2I!

Революционный B2I Инструмент анализа файлов™ сканирует, анализирует и сообщает подробную информацию о файле B2I. Наш алгоритм (ожидается выдача патента) быстро проанализирует файл и через несколько секунд предоставит подробную информацию в наглядном и легко читаемом формате.†

Уже через несколько секунд вы точно узнаете тип вашего файла B2I, приложение, сопоставленное с файлом, имя создавшего файл пользователя, статус защиты файла и другую полезную информацию.

Чтобы начать бесплатный анализ файла, просто перетащите ваш файл B2I внутрь пунктирной линии ниже или нажмите «Просмотреть мой компьютер» и выберите файл. Отчет об анализе файла B2I будет показан внизу, прямо в окне браузера.

Ваш файл анализируется... пожалуйста подождите.

Имя файла:

Размер файла:

Прервать

† Инструмент анализа файлов B2I использует компоненты стороннего программного обеспечения. Нажмите здесь, чтобы прочитать правовую оговорку.

Об авторе: Джей Гитер (Jay Geater) является президентом и генеральным директором корпорации Solvusoft — глобальной компании, занимающейся программным обеспечением и уделяющей основное внимание новаторским сервисным программам. Он всю жизнь страстно увлекался компьютерами и любит все, связанное с компьютерами, программным обеспечением и новыми технологиями.

www.solvusoft.com

Что такое уровни знания английского языка CEFR (A1, B2 и т.д.)

Как вы определяете свой уровень владения английским? Говорите «Хороший», «Ну так… средненько». Используете названия ступеней на английском: «Intermediate, пожалуй, будет»? Или вспоминаете классическую формулу «читаю и перевожу со словарем»?

Если вы сталкивались с ситуацией, где нужна оценка уровня английского языка, если вы обращаетесь на курсы иностранных языков, если просто у вас есть знакомый преподаватель, то вы наверняка встречали загадочные слова A1, B2, C1. Что это? Морской бой на очень маленьком поле? Не совсем. Это так называемые уровни CEFR – шкалы, используемой в Европе для определения уровня владения языком.

История CEFR

Знание языка на определенном уровне может быть совсем разным для разных языков. Неудивительно, ведь все языки разные – в одном есть развитая система грамматических времен, но совсем нет сложной морфологии, т.е. разных форм слов. В другом – всего три времени, но вот над падежами и склонениями придется попотеть. В третьем – грамматика примитивна, но каждое слово – это не набор букв, а уникальная картинка (иероглиф). Понятно, что для каждого из них «я знаю этот язык на среднем уровне» означает совсем разный набор умений и навыков.

В каждой стране определением уровней занималась отдельная организация (обычно, самая уважаемая в деле изучения языков) – институт Сервантеса в Испании, институт Гете в Германии, Кембридж в Великобритании. Учебники и курсы, тесты и экзаменов, соответственно, разрабатывались под эти уровни, индивидуальные для каждого языка. При этом сравнить знание английского на уровне intermediate, немецкого на уровне Mittelstufe и китайского на уровне «чунгденг» было достаточно сложно.

И вот в 1991 году в Швейцарии (что не случайно – это страна с 4 государственными языками) на научном симпозиуме было принято решение разработать универсальную шкалу, которую можно будет использовать для оценки уровней знания любого языка. Долго ли, коротко (наука – дело небыстрое), к 2003 году был запущен пилотный проект такой шкалы, а в 2007 году финальная версия шкалы CEFR была официально представлена на конференции в Кембридже. В последующие годы основные курсы и экзамены всех европейских языков (и некоторых неевропейских) были поставлены в соответствие с новой шкалой.

Как устроена CEFR

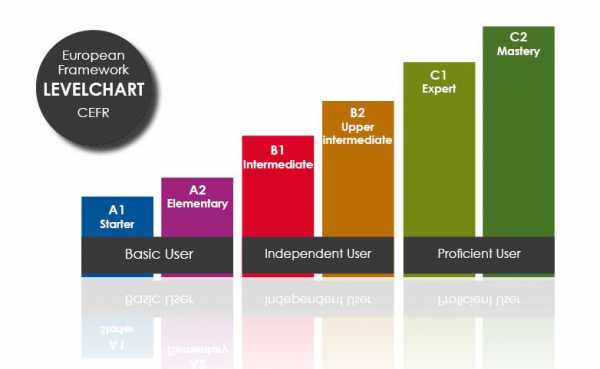
Сама шкала состоит из 3 больших уровней знания языка: A, B и C – или еще они называются, соответственно, Basic user (базовый, вы начинаете понимать), Independent user (независимый, вы начинаете доносить практически любую мысль), Proficient user (свободный, вы приближаетесь к носителям языка). Каждый из этих уровней разбивается еще на два, которые уже обозначаются буквами – получаются A1, A2, B1, B2, C1, C2 – 6 уровней.

CEFR использует так называемый action-oriented approach, т.е. «ориентированный на действие». То есть для определения уровня используются не знание каких-то специальных грамматических структур или наборов слов, а «что может сделать». Не «выучил present perfect и 100 слов из темы ‘мой город’», а «может понять основную мысль при общении на знакомые темы – работа, школа, досуг».

Вот как, например, выглядит такое «могу сделать» для уровня А2:

Понимаю отдельные предложения и часто встречающиеся выражения, связанные с основными сферами жизни (например, основные сведения о себе и членах своей семьи, покупках, устройстве на работу и т. п.). Могу выполнить задачи, связанные с простым обменом информацией на знакомые или бытовые темы. В простых выражениях могу рассказать о себе, своих родных и близких, описать основные аспекты повседневной жизни.

Видите, «могу рассказать о себе и близких» – и не так уж важно, какое грамматическое время вы будете использовать, главное, чтобы собеседник вас понял – ведь в этом и есть конечная цель владения иностранным языком – обмениваться информацией, а не учить правила.

Аспекты владения языком (чтение, письмо и т.д.)

Шкала CEFR дает не только общую картину того, что студент может делать на каждом из уровней, но и дает подробное описание для всех 5 составляющих языка: понимание письменной и устной речи, умение говорить на языке, умение использовать язык для разговора, письмо.

Вот как выглядит, например, по шкале CEFR, понимание письменной речи (т.е. чтение) для того же уровня А2:

Я понимаю очень короткие простые тексты. Я могу найти конкретную, легко предсказуемую информацию в простых текстах повседневного общения: в рекламах, проспектах, меню, расписаниях. Я понимаю простые письма личного характера.

Ссылки на полный список всех навыков для всех уровней – внизу страницы.

Время, необходимое, чтобы выучить английский до определенного уровня

Шкала CEFR помогает дать ответ и на частый вопрос «сколько времени нужно, чтобы выучить английский». Это зависит от того, какого уровня вы хотите достичь. Каждый следующий уровень достичь примерно вдвое сложнее предыдущего. Технические специалисты вспомнят при этом слово «логарифмический», а для всех остальных объясню на простых цифрах: чтобы достичь уровня A1, необходимо около 100 часов занятий, чтобы подняться с A1 до A2 – нужно около 200 часов занятий, с B1 до B2 – около 600, с C1 до C2 – 1200. Цифры очень условные – все зависит от студента, от преподавателя, от мотивации, выполнения домашних заданий и еще десятков факторов.

CEFR и традиционные названия уровней

После появления шкалы CEFR, к ней были приведены многие стандарты владения иностранными языками. Были поставлены в соответствие с CEFR и старые привычные названия уровней. Вот они:

A1 – Beginner
A2 – Elementary
иногда используемая ступень Pre-intermediate находится между A2 и B1
B1 – Intermediate
B2 – Upper-intermediate
C1 – Advanced
C2 – Upper-Advanced или Proficiency

Итак, уровни от A1 до С2, о которых вы могли слышать от знакомых преподавателей или представителей языковых школ – это уровни знания языка по так называемой шкале CEFR, или, как ее еще называются «Общеевропейской шкалой языковых компетенций». Эта шкала основана не на знаниях каких-то наборов слов или грамматических конструкций, а на том, что может сделать изучающий язык на том или ином уровне. Именно поэтому шкала CEFR универсальна – ее можно применить к любому языку.

Дополнительная информация

Полный текст монографии о CEFR (на английском языке)http://www.coe.int/t/dg4/linguistic/Source/Framework_EN.pdf

Компетенции CEFR (на русском языке)http://lang.mipt.ru/articles/european_levels.html

Википедия о CEFR (на английском)http://en.wikipedia.org/wiki/Common_European_Framework_of_Reference_for_Languages

Википедия о CEFR (на русском)http://ru.wikipedia.org/wiki/Общеевропейские_компетенции_владения_иностранным_языком

Статьи по теме:

english99.ru

§7. Примеры решения типовых задач

В данном параграфе рассмотрим задачи, связанные с различными системами координат, делением отрезка в заданном отношении.

Пример 1.

Даны координаты точек: А(4; 3), В(7; 6), С(2; 11). Докажем, что треугольник АВС прямоугольный.

Найдем длины сторон треугольника АВС. С этой целью используем формулу, позволяющую находить расстояние между двумя точками на плоскости:

Длины сторон будут равны:

Учитывая, что для сторон данного треугольника выполняется теорема Пифагора

то треугольник АВС – прямоугольный.

Пример 2.

Даны точки А(2; 1) и В(8; 4). Найдем координаты точки М(х; у), которая делит отрезок в отношении 2:1.

Напомним, что точка М(х; у) делит отрезок АВ, где A(xA, yA), B(xB, yB), в отношении λ : μ, если ее координаты удовлетворяют условиям:

, .

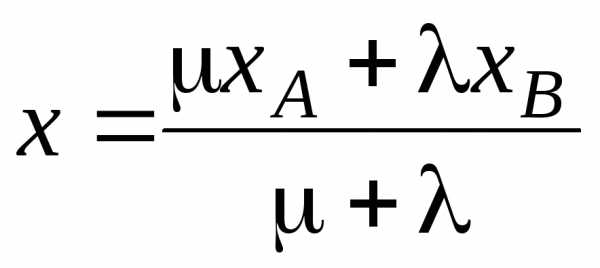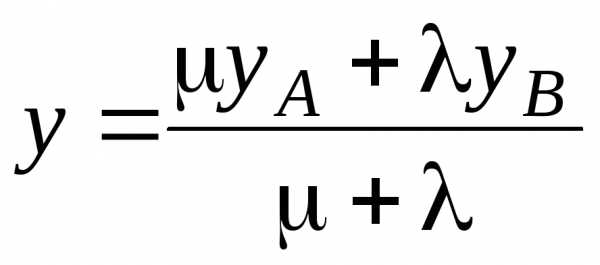Найдем точку М для данного отрезка

, .

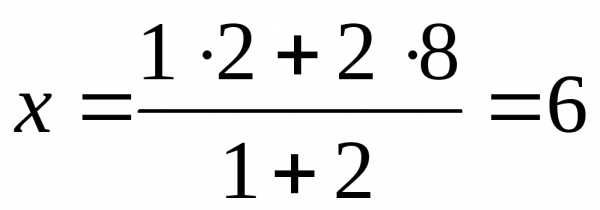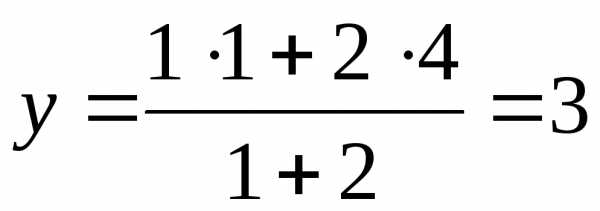Таким образом, точка М(6; 3) делит отрезок АВ в отношении 2:1.

Пример 3.

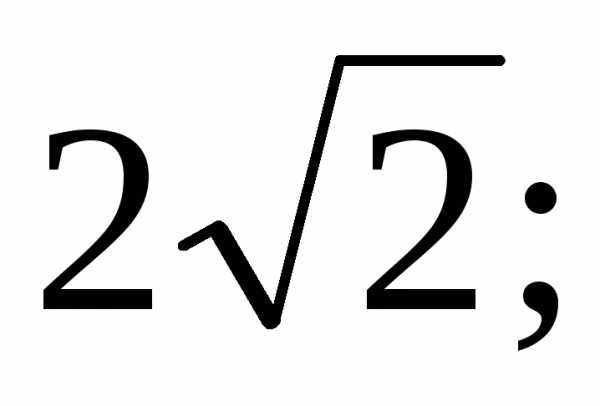Найдем прямоугольные координаты точки А(

3π/4), если полюс совпадает с началом координат, а полярная ось направлена по оси абсцисс.

Учитывая формулы перехода от полярной к прямоугольной системе координат

x = r cosφ, y = r sinφ,

получаем

В прямоугольной декартовой системе координат координаты точки А(–2; 2).

Пример 4.

Найдем полярные координаты точек, имеющих следующие прямоугольные координаты:

А(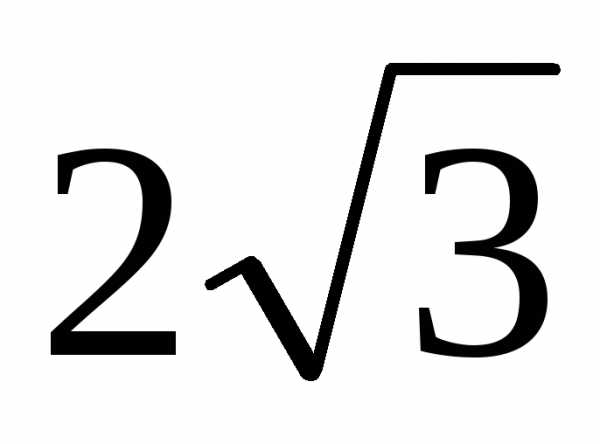; 2),В(–4; 4), С(–7; 0).

Используем формулы перехода от прямоугольных координат к полярным:

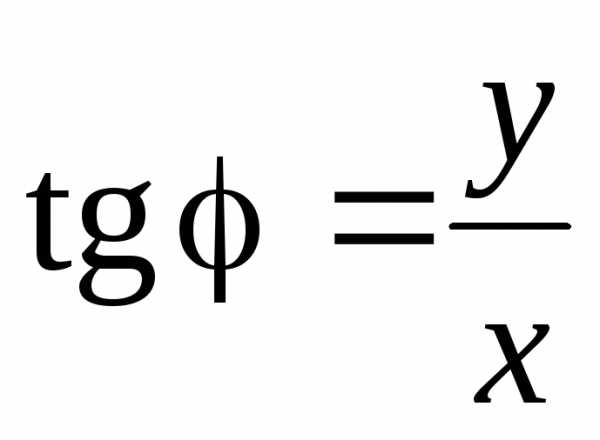Получим координаты для точки А:

, .

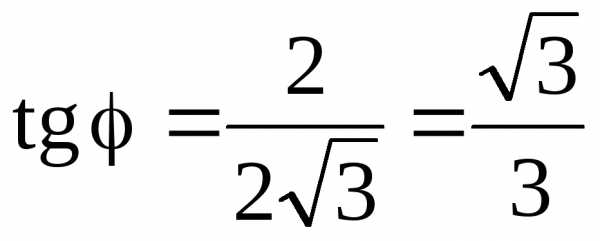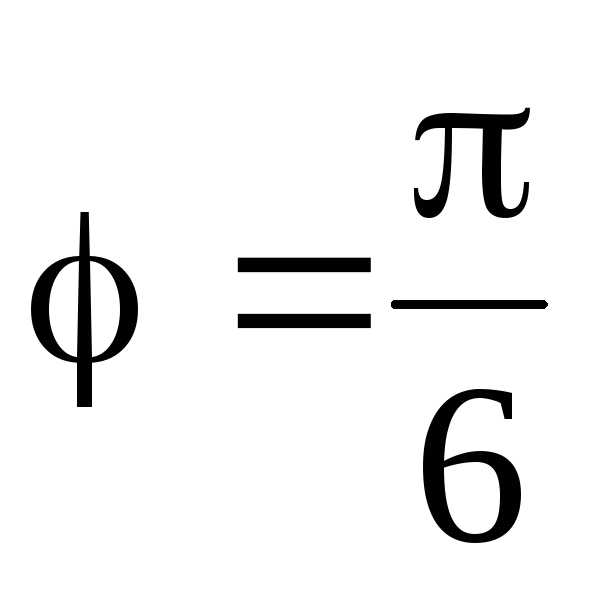Таким образом А(4; π/6) – полярные координаты (рис. 15).

Для точки В (рис. 16) имеем

, .

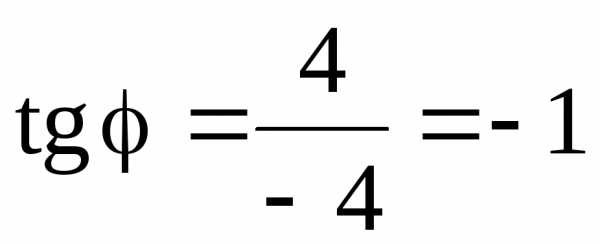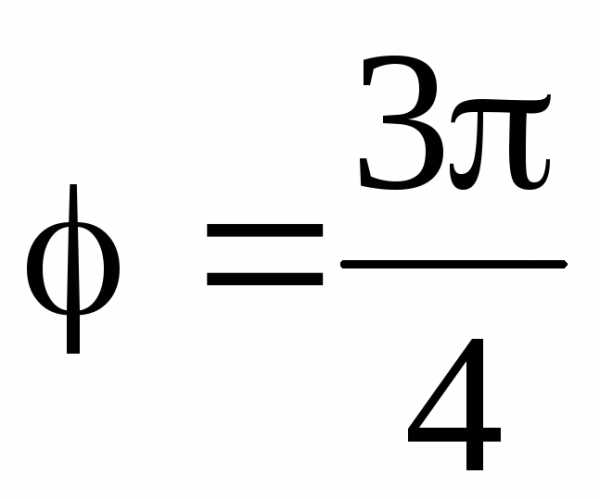Следовательно, полярные координаты точки В(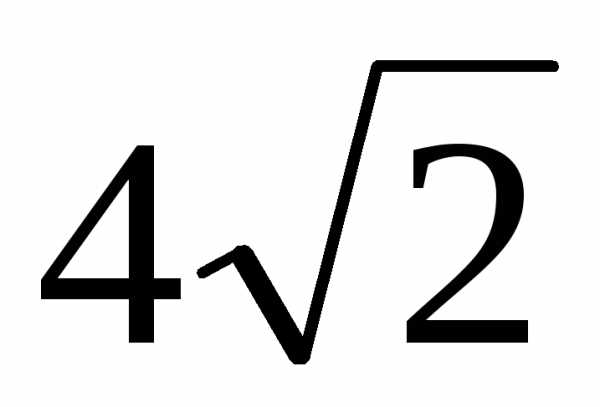, 3π/4).

Рассмотрим точку С(–7; 0) (рис. 17). В этом случае

, .

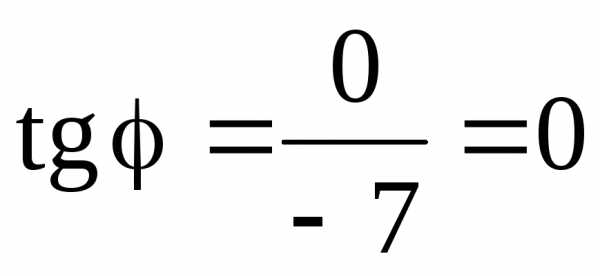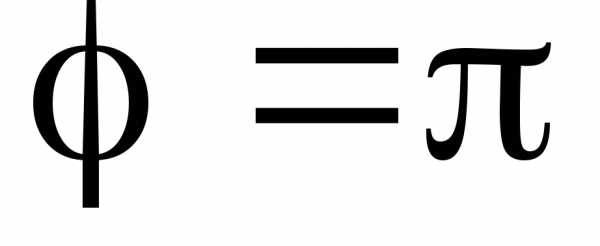Можно записать полярные координаты точки С(7; π).

Пример 5.

Найдем длину вектора a = 20i + 30j – 60k и его направляющие косинусы.

Напомним, что направляющие косинусы – это косинусы углов, которые вектор a(a1, a2, a3) образует с осями координат:

, ,,

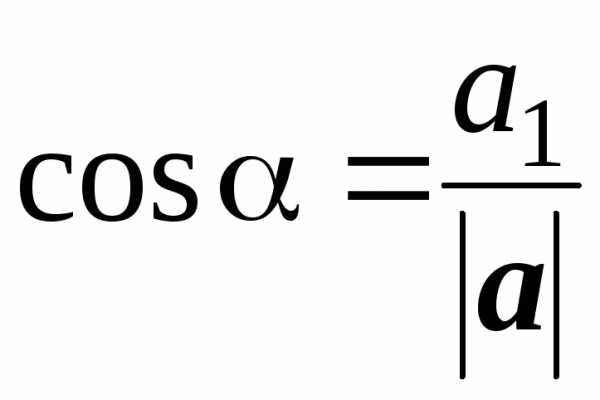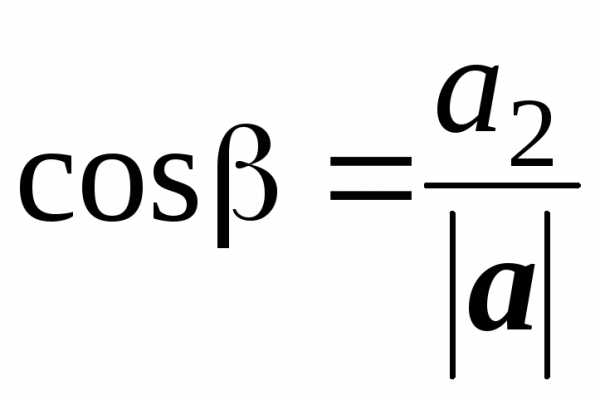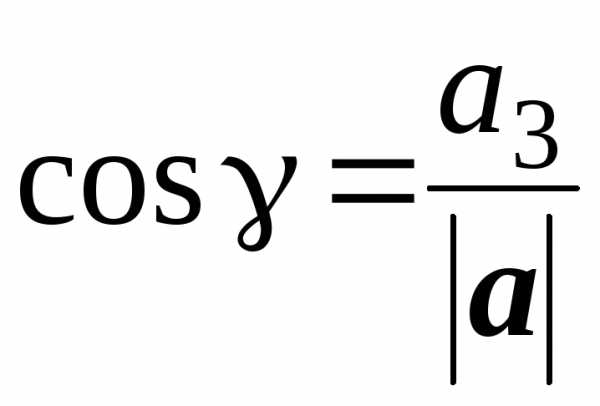где .

Применим эти формулы к данному вектору, получим

Пример 6.

Нормируем вектор a = 3i + 4j – 12k.

Нормировать вектор – это найти вектор единичной длины а0, направленный также как и данный вектор. Для произвольного вектора a(a1, a2, a3) соответствующий вектор единичной длины можно найти, умножив a на дробь .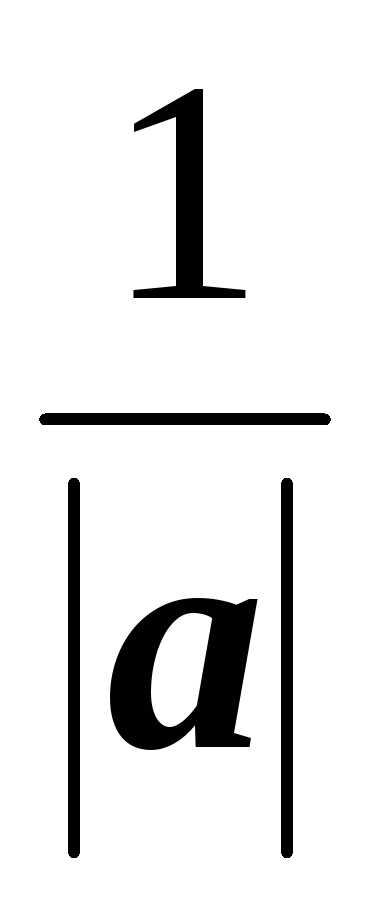

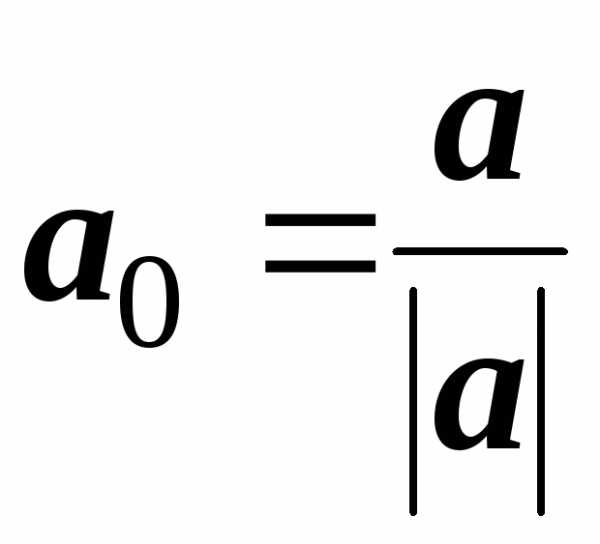В нашем случае и вектор единичной длины:

Пример 7.

Найдем скалярное произведение векторов

a = 4i + 5j + 6k и b = 3i – 4j + k.

Для того чтобы найти скалярное произведение векторов, нужно умножить соответствующие координаты и полученные произведения сложить. Так, для векторов a = a1i + a2j + a3k и b = b1i + b2j + b3k скалярное произведение имеет вид:

(a, b) = a1b1 + a2b2 + a3b3.

Для данных векторов получаем

(a, b) = 4∙3 + 5∙(–4) + 6∙1 = 12 – 20 + 6 = –2.

Пример 8.

Покажем, что векторы a = 2i – 3j + 5k и b = i + 4j + 2k перпендикулярны.

Два вектора перпендикулярны, если их скалярное произведение равно нулю.

Найдем скалярное произведение:

(a, b) = 2∙1 + (–3)∙4 + 5∙2 = 2 – 12 + 10 = 0.

Таким образом, векторы а и b перпендикулярны.

Пример 9.

Выясним, при каком значении параметра m векторы a = 2i + 3j + mk и b = 3i + mj – 2k перпендикулярны.

Найдем скалярное произведение векторов а и b:

(a, b) = 2∙3 + 3∙m – 2∙m = 6 + m.

Векторы перпендикулярны, если их скалярное произведение равно нулю. Приравниваем к нулю произведение (а, b):

6 + m = 0.

При m = – 6 векторы а и b перпендикулярны.

Пример 10.

Найдем скалярное произведение (3а + 4b, 2а – 3b), если |a| = 2, |b| = 1 и угол φ между а и b равен π/3.

Воспользуемся свойствами скалярного произведения:

(αa, βb) = αβ(a, b),

(a + b, c) = (a, c) + (b, c),

(a, b) = (b, a)

(a, a) = |a|2,

а также определением скалярного произведения (a, b) = |a|∙|b|∙cosφ. Перепишем скалярное произведение в виде

(3a + 4b, 2a – 3b) = 6(a, a) – 9(a, b) + 8(b, a) – 12(b, b) =

= 6|a|2 – (a, b) – 12|b|2 = 6∙22 – 2∙1∙cos(π/3) – 12∙12 = 11.

Пример 11.

Определим угол между векторами

a = i + 2j + 3k и b = 6i + 4j – 2k.

Для нахождения угла воспользуемся определением скалярного произведения двух векторов

(a, b) = |a|∙|b|∙cosφ,

где φ – угол между векторами а и b. Выразим cosφ из этой формулы

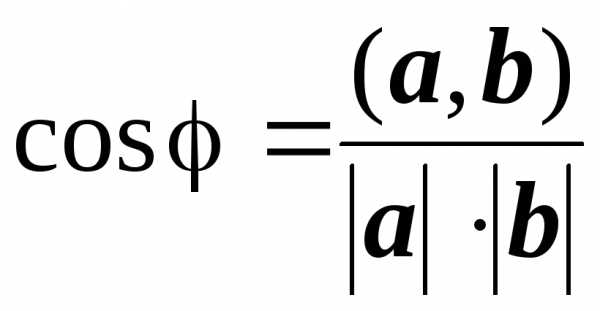Учитывая, что (а, b) = 1∙6 + 2∙4 + 3∙(–2) = 8, ,, получаем:

Следовательно, .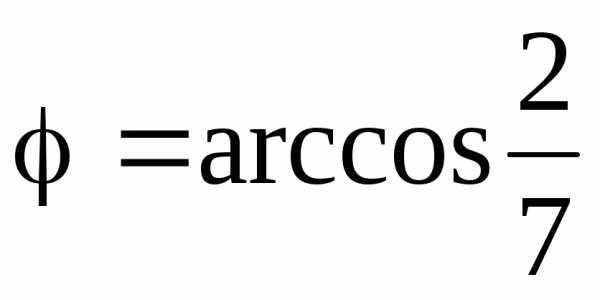

Пример 12.

Найдем векторное произведение векторов

a = 5i – 2j + 3k и b = i + 2j – 4k.

Известно, что векторное произведение векторов a = a1i + a2j + a3k и b = b1i + b2j + b3k находится по формуле

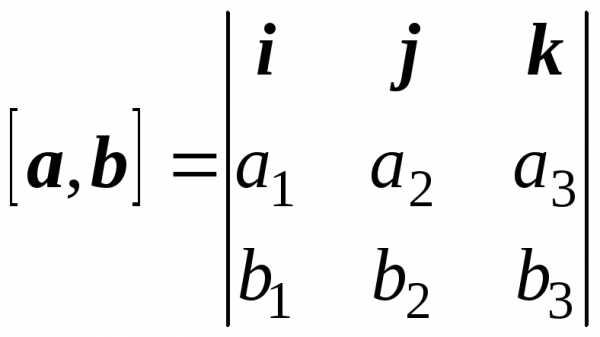Следовательно, для данных векторов

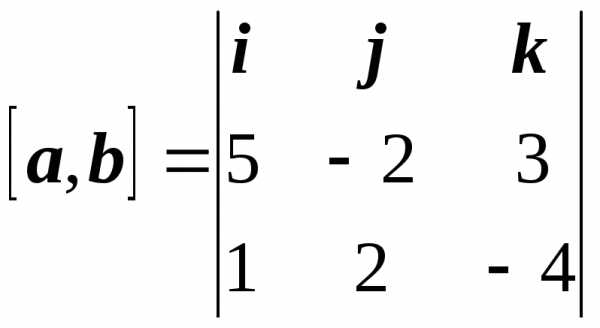
= 2i + 23j + 12k.

Рассмотрим пример, где для нахождения модуля векторного произведения будет использоваться определение векторного произведения, а не выражение его через координаты сомножителей, как было в предыдущем примере.

Пример 13.

Найдем модуль векторного произведения векторов а + 2b и 2а – 3b, если |a| = 1, |b| = 2 и угол между векторами а и b равен 30°.

Из определения векторного произведения видно, что для произвольных векторов а и b его модуль равен

|[a, b] | = |a| ∙ |b| ∙ sin φ.

Учитывая свойства векторного произведение

[a, b] = – [b, a],

[a, a] = 0,

[αa + βb, c] = α[a, c] + β[b, c],

получаем

[a + 2b, 2a – 3b] = 2[a, a] – 3[a, b] + 4[b, a] – 6[b, b] = –7[a, b].

Значит, модуль векторного произведения равен

|[a + 2b, 2a – 3b]| = |–7[a, b]| = 7 ∙ |a| ∙ |b| ∙ sin 30° = 7∙1∙2∙0,5 = 7.

Пример 14.

Вычислим площадь параллелограмма, построенного на векторах

a = 6i + 3j – 2k и b = 3i – 2j + 6k.

Известно, что модуль векторного произведения двух векторов равен площади параллелограмма, построенного на этих векторах. Найдем векторное произведение по формуле:

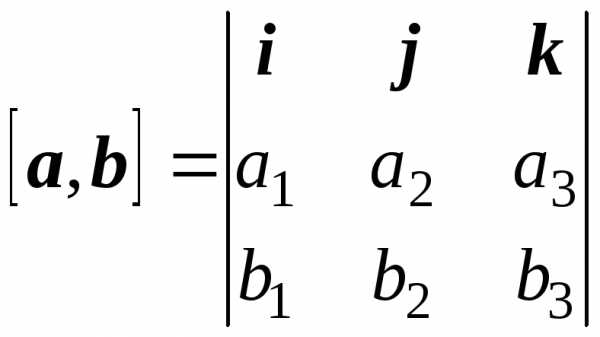где a = a1i + a2j + a3k и b = b1i + b2j + b3k. Затем вычислим его модуль.

Для данных векторов получаем

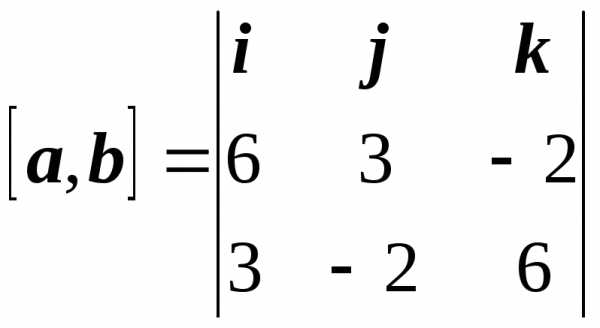
= 14i – 42j – 21k.

Следовательно, площадь параллелограмма равна

S = |[a, b]| = (кв. ед.).

Пример 15.

Вычислим площадь треугольника с вершинами А(1;2;1), В(3;3;4), С(2;1;3).

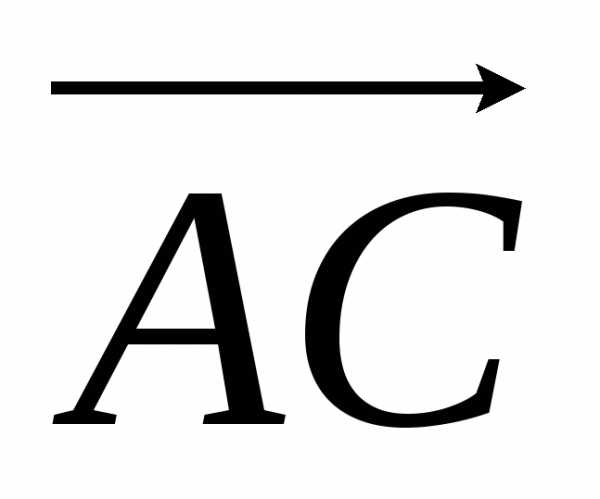
Очевидно, что площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах 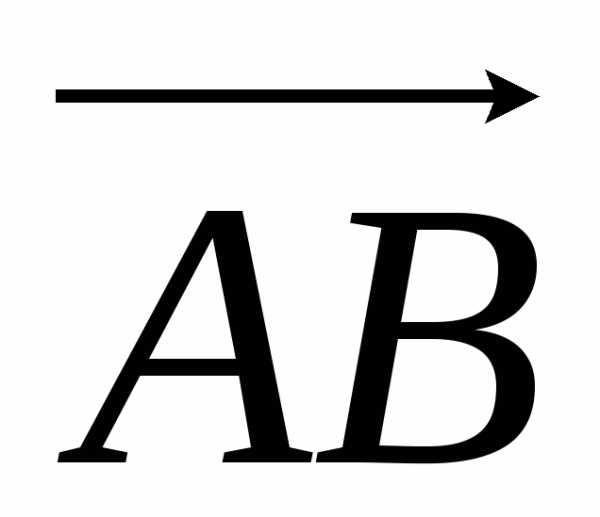и.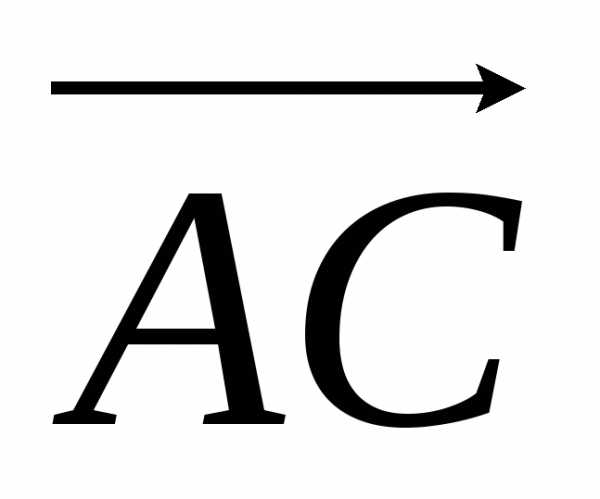

В свою очередь, площадь параллелограмма, построенного на векторах 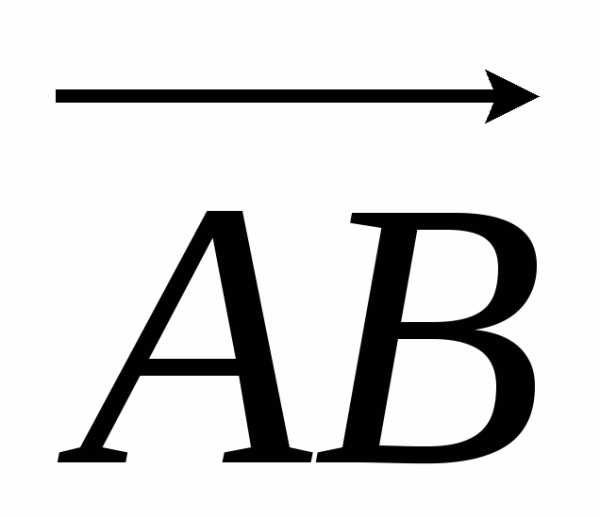и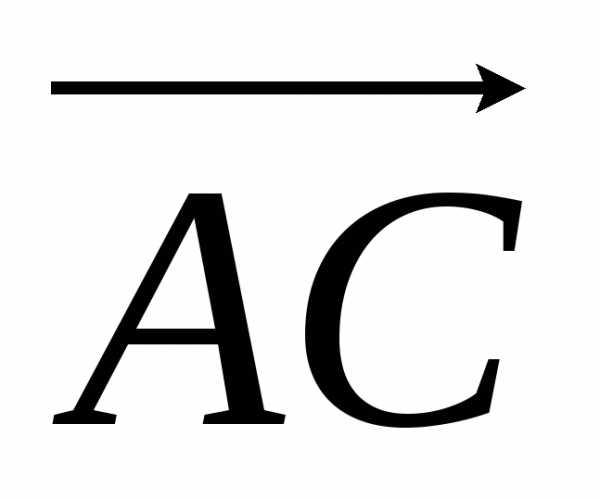, равна модулю векторного произведения [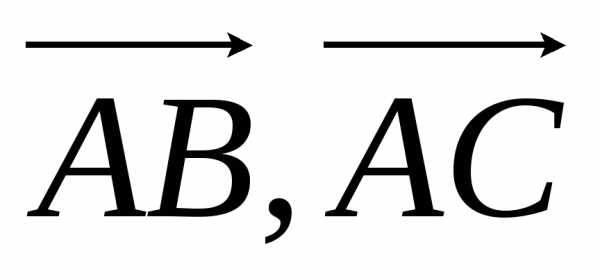]. Таким образом

|[]|.

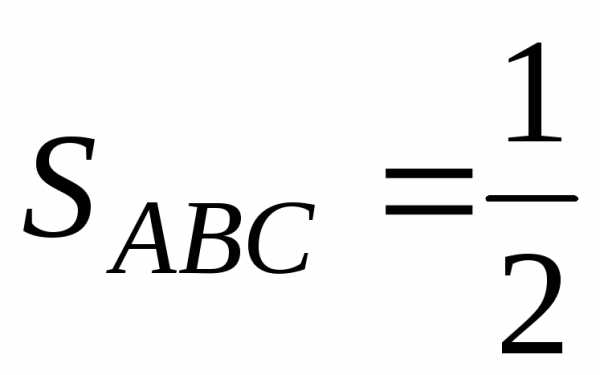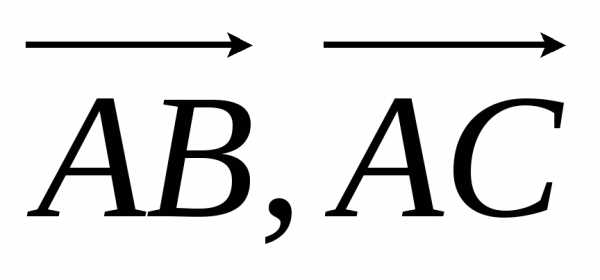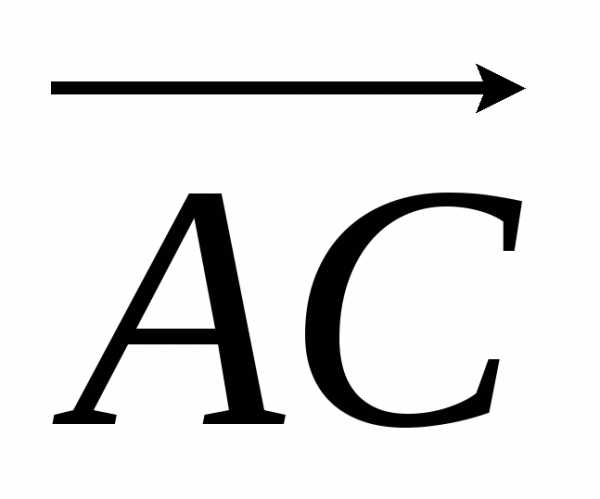
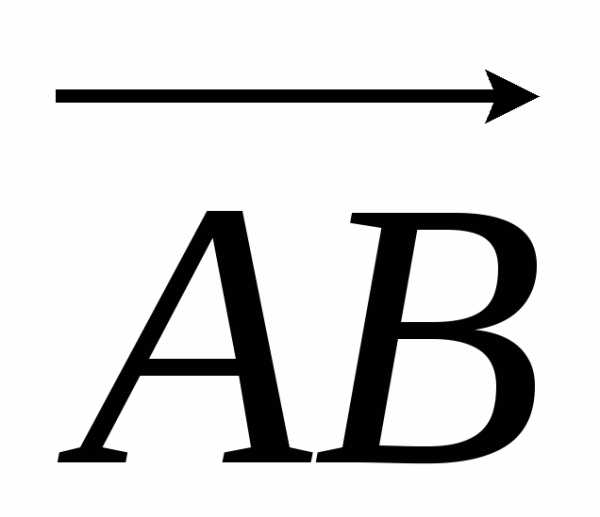
Найдем координаты векторов 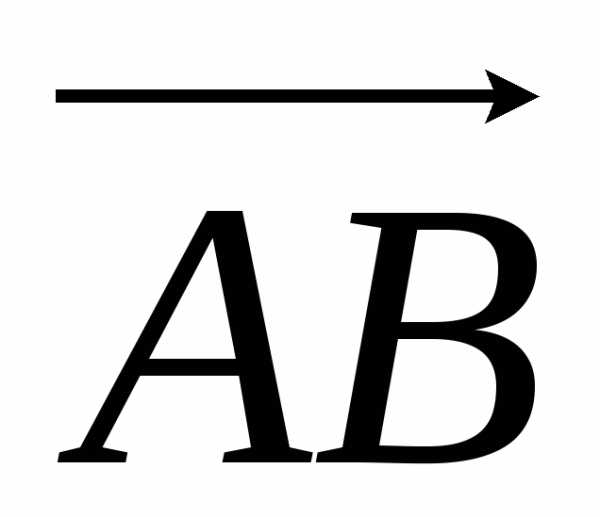и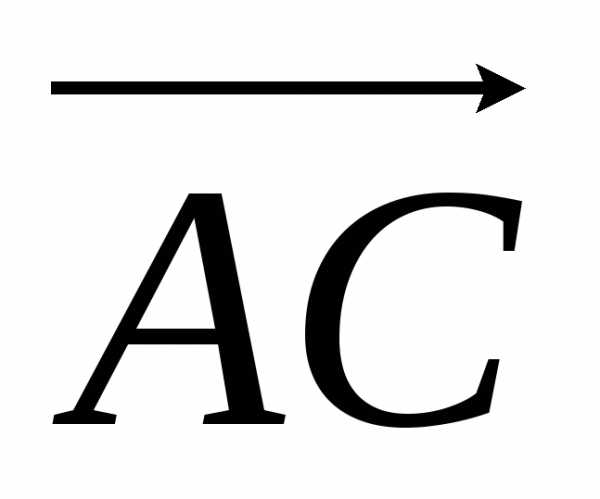, вычитая из координат конца вектора соответствующие координаты начала, получим

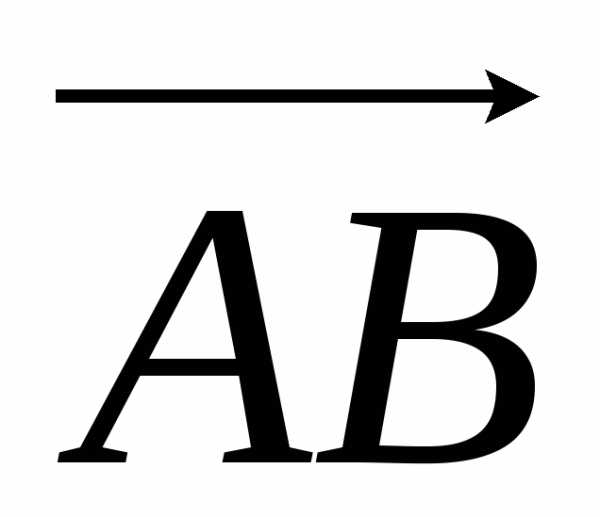= (3 – 1)i + (3 – 2)j + (4 – 1)k = 2i + j + 3k,

= (2 – 1)i + (1 – 2)j + (3 – 1)k = i – j + 2k.

Найдем векторное произведение:

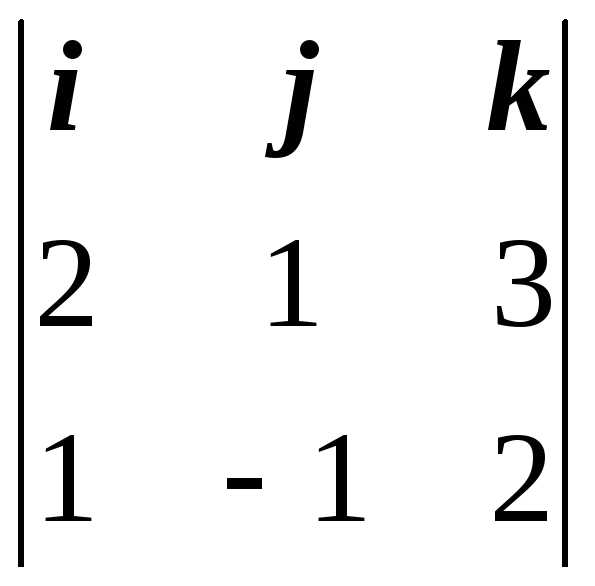[,] = 5i – j – 3k.

Найдем модуль векторного произведения:

|[]| = .

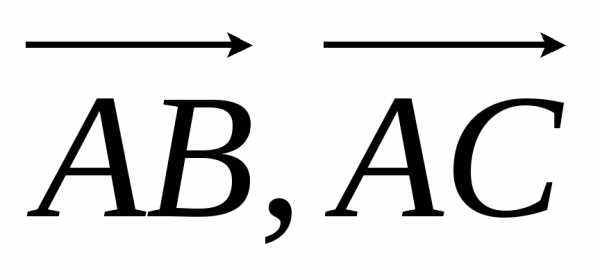Следовательно, можем получить площадь треугольника:

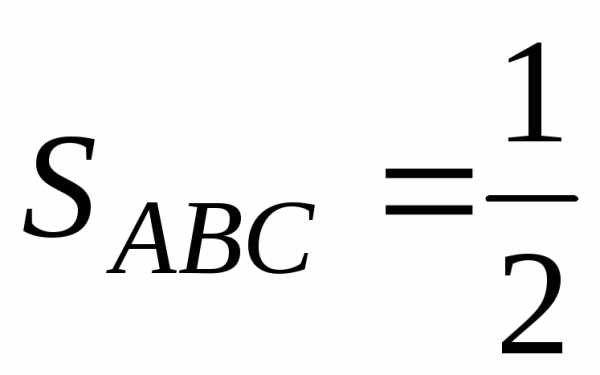
(кв. ед.).

Пример 16.

Вычислим площадь параллелограмма, построенного на векторах a + 3b и 3a – b, если |a| = 2, |b| = 1 и угол между а и b равен 30°.

Найдем модуль векторного произведения, используя его определение и свойства, указанные в примере 13, получим

[a + 3b, 3a – b] = 3[a, a] – [a, b] + 9[b, a] – 3[b, b] = –10[a, b].

Значит, искомая площадь равна

S = |[a + 3b, 3a – b]| = |–10[a, b]| = 10 ∙ |a| ∙ |b| ∙ sin 30° =

= 10∙2∙1∙0,5 = 10 (кв. ед.).

Следующие примеры будут связаны с использованием смешанного произведения векторов.

Пример 17.

Показать, что векторы a = i + 2j – k, b = 3i + k и с = 5i + 4j – k компланарны.

Векторы компланарны, если их смешанное произведение равно нулю. Для произвольных векторов

a = a1i + a2j + a3k, b = b1i + b2j + b3k, c = c1i + c2j + c3k

смешанное произведение находим по формуле:

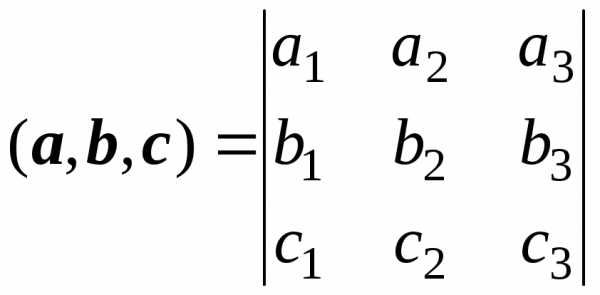Для данных векторов получаем

Таким образом, данные векторы компланарны.

Пример18.

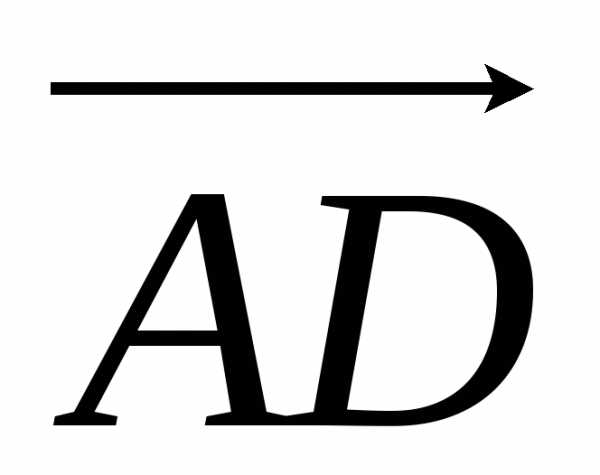
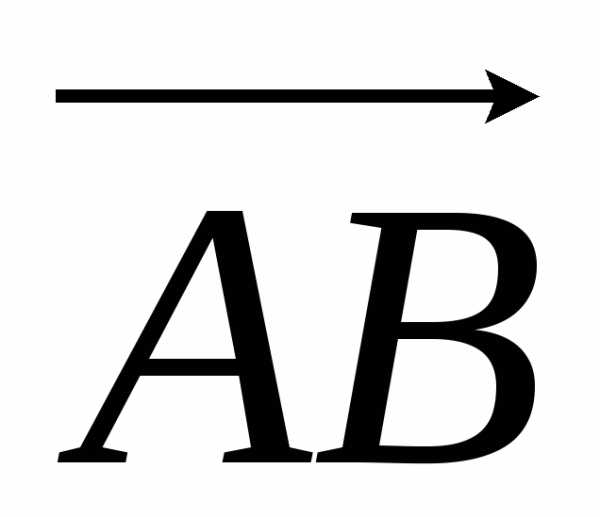
Найдем объем треугольной пирамиды с вершинами А(1;1;1), В(3;2;1), С(2;4;3), D(5;2;4).

Найдем координаты векторов 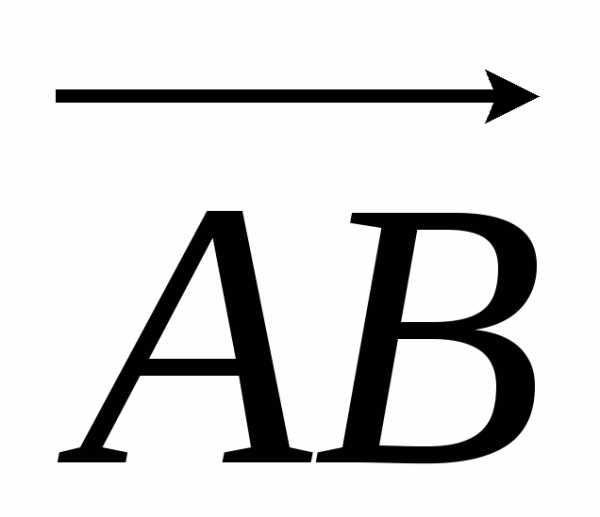,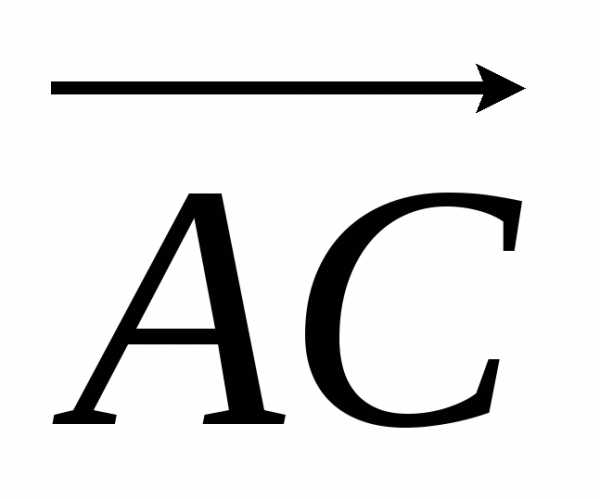и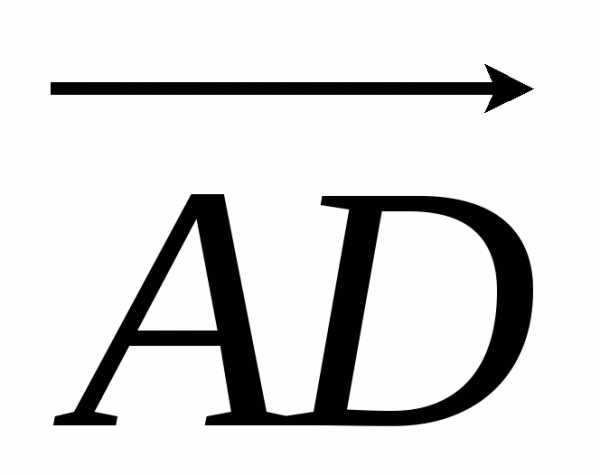, совпадающих с ребрами пирамиды. Вычитая из координат конца вектора соответствующие координаты начала, получаем

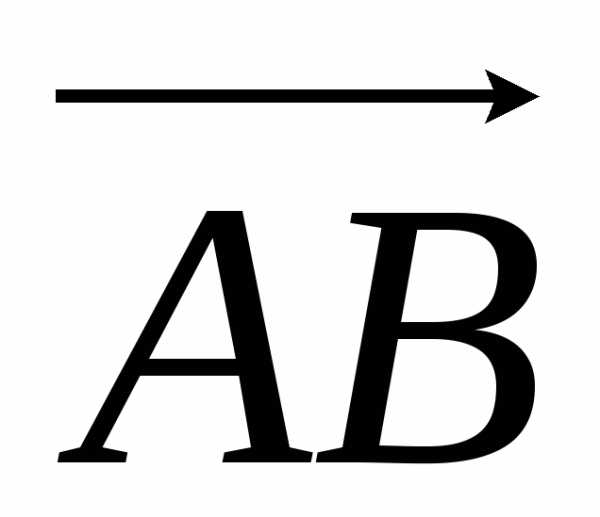= 2i + 3j,

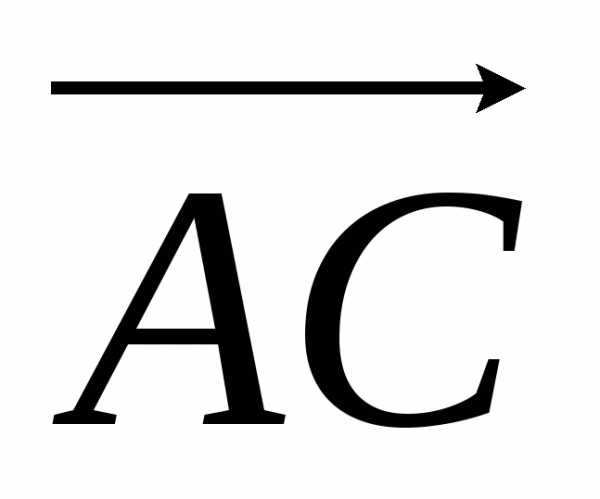= i + 3j + 2k,

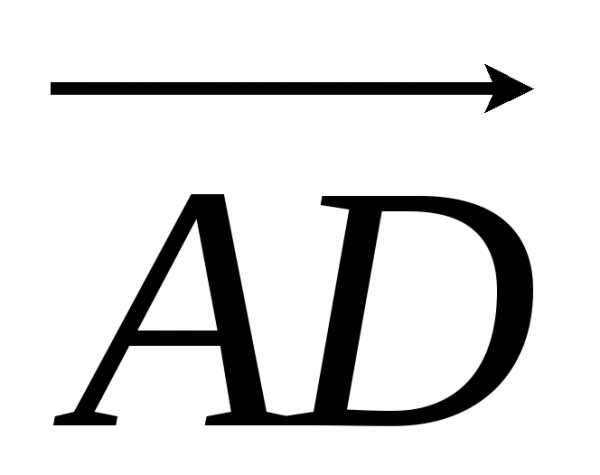= 4i + j + 3k.

Известно, что объем пирамиды равен 1/6 объема параллелепипеда, построенного на векторах 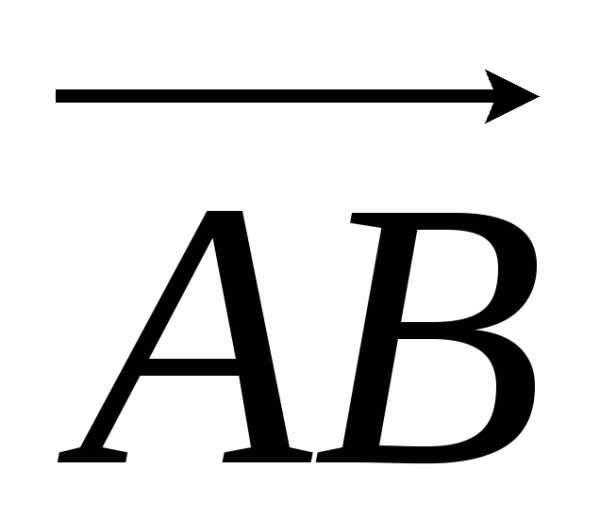,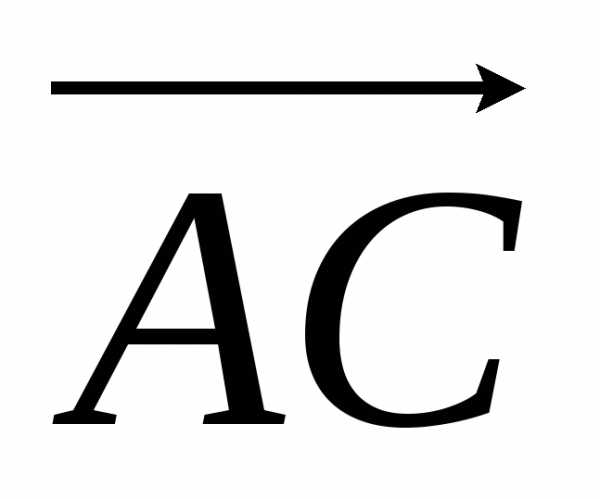и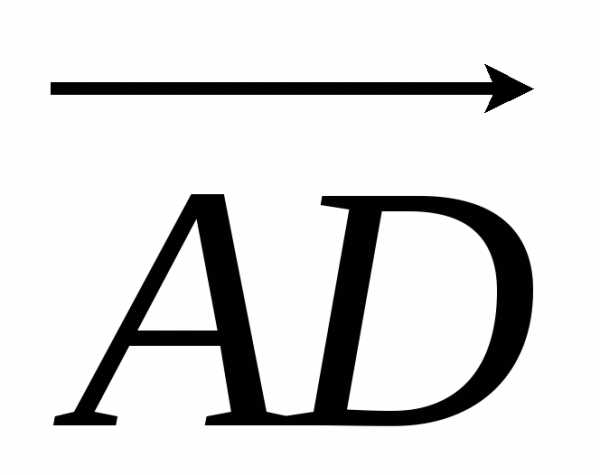. Таким образом,

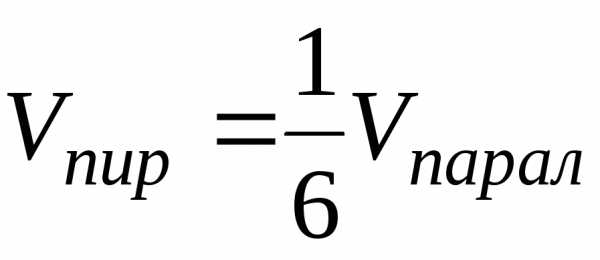В свою очередь, объем параллелепипеда равен модулю смешанного произведения

Vпарал = |(,,)|.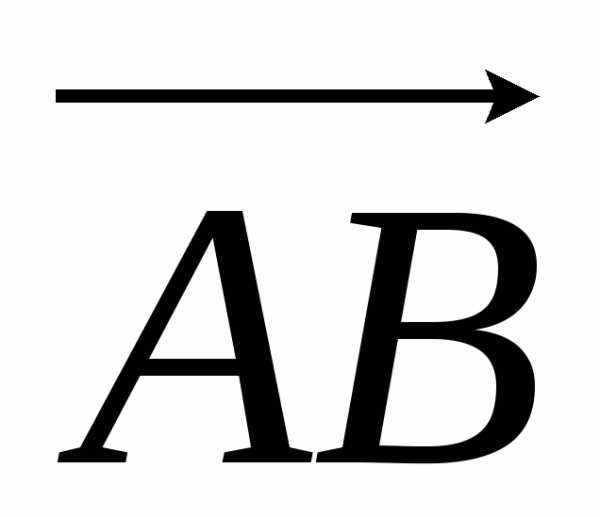

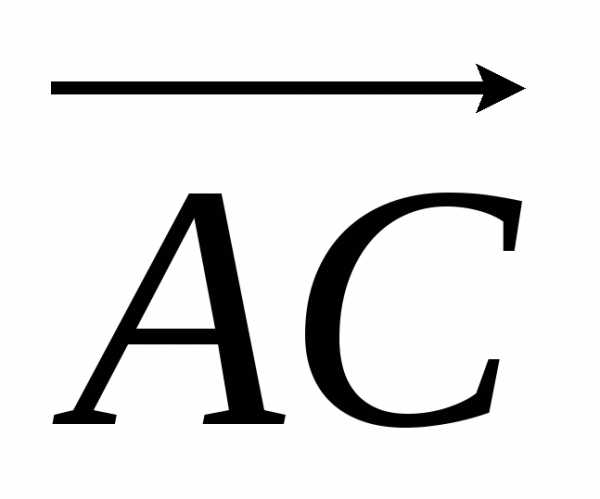Найдем смешанное произведение

(,,) = .

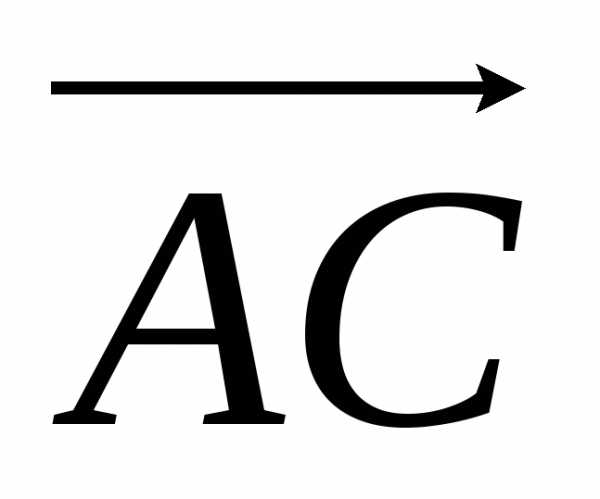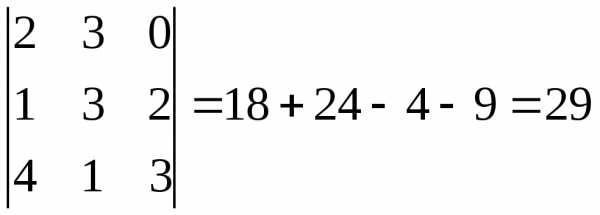Итак, объем пирамиды равен

(куб. ед.).

В следующих примерах покажем возможное применение векторной алгебры.

Пример 19.

Проверим, являются ли коллинеарными вектора 2а + b и а – 3b, где a = 2i + j – 3k и b = i + 2j + 4k.

Найдем координаты векторов 2а + b и а – 3b:

2а + b = 2(2i + j – 3k) + i + 2j + 4k = 5i + 4j – 2k,

а – 3b = 2i + j – 3k – 3(i + 2j + 4k) = –i – 5j – 15k.

Известно, что у коллинеарных векторов пропорциональные координаты. Учитывая, что

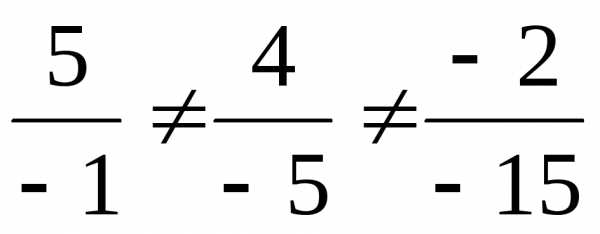получаем, что вектора 2а + b и а – 3b неколлинеарны.

Эту задачу можно было решить и другим способом. Критерием коллинеарности векторов является равенство нулю векторного произведения:

[2a + b, a – 3b] = 2[a, a] – 6[a, b] + [b, a] – 3[b, b] = –7[a, b].

Найдем векторное произведение векторов а и b:

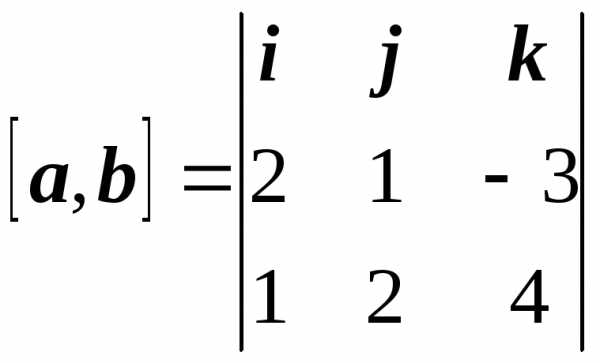
= 10i – 11j + 3k ≠ 0.

Следовательно,

[2a + b, a – 3b] = –7[a, b] ≠ 0

и векторы 2а + b и а – 3b неколлинеарны.

Пример 20.

Найдем работу силы F(3; 2; 1), когда точка ее приложения А(2; 4;–6), двигаясь прямолинейно, перемещается в точку В(5; 2; 3).

Известно, что работа силы – это скалярное произведение силы F на вектор перемещения .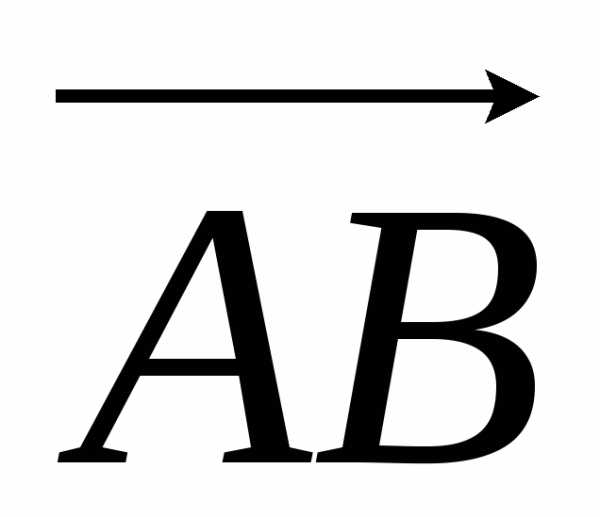

Найдем координаты вектора :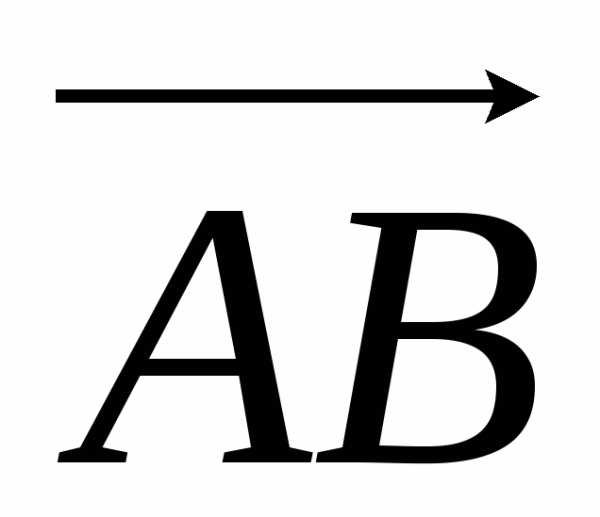

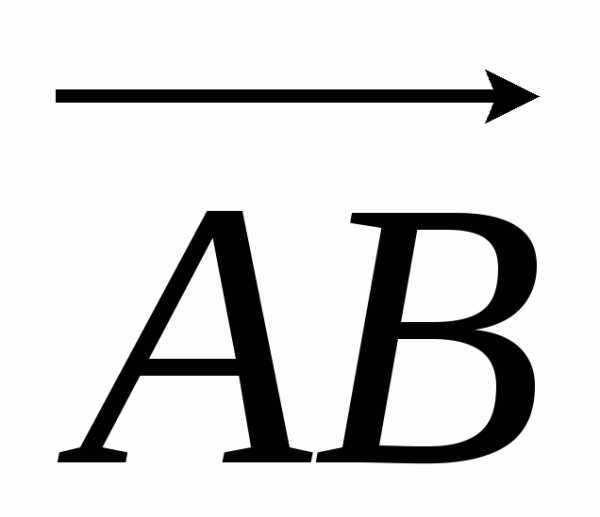= 3i – 2j + 9k.

Следовательно, работа силы F по перемещению точки А в точку В будет равна скалярному произведению

(F, 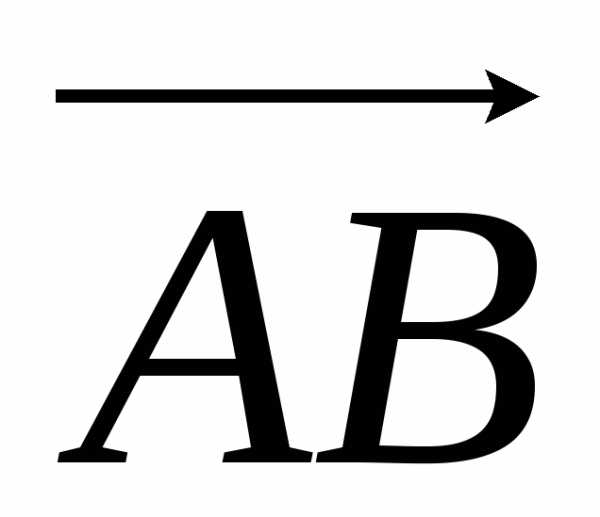) = 3∙3 + 2∙(–2) + 1∙9 = 9 – 4 + 9 = 14.

Пример 21.

Пусть сила F( 2;3;–1) приложена к точке А(4;2;3). Под действием силы F точка А перемещается в точку В(3;1;2). Найдем модуль момента силы F относительно точки В.

Известно, что момент силы равен векторному произведению силы на перемещение. Найдем вектор перемещения :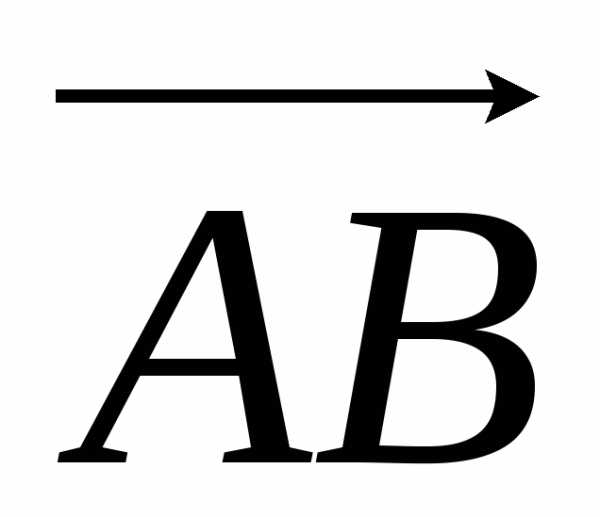

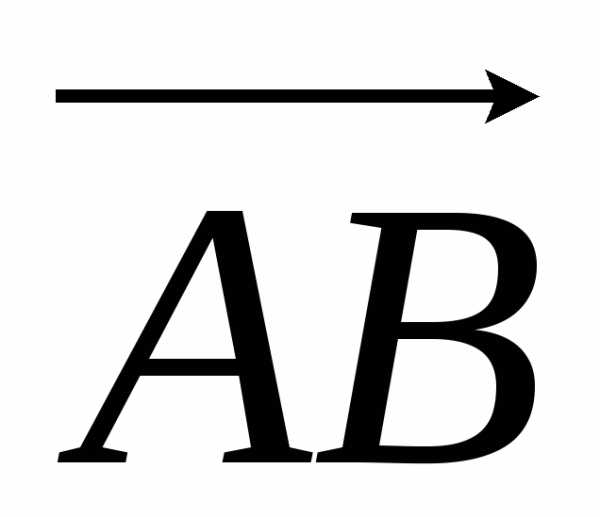= (3 – 4)i + (1 – 2)j + (2 – 3)k = – i – j – k.

Найдем момент силы как векторное произведение:

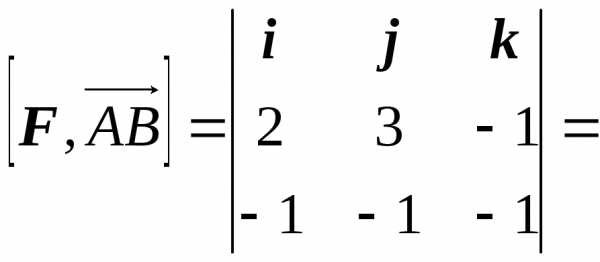
= – 4i + 3j + k.

Следовательно, модуль момента силы равен модулю векторного произведения:

|[F, ]| = .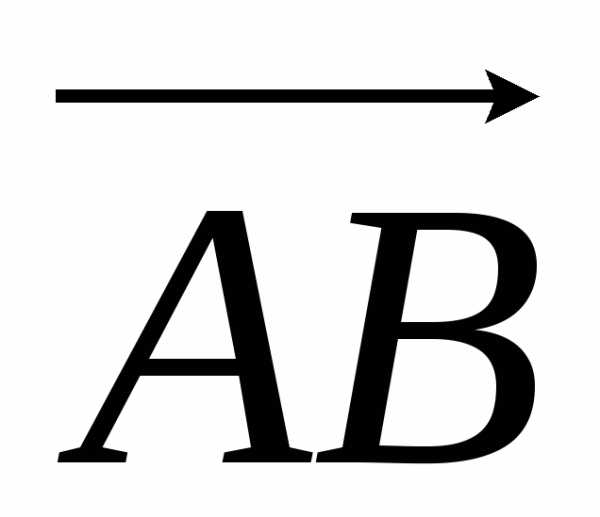

studfiles.net