Он-лайн консультация

Основные способы посчитать проценты - вручную, на калькуляторе или в программе. Формула расчет процентов

Как найти процент от числа

Процент — это одна сотая часть заданного числа или величины. Указывается знаком «%».

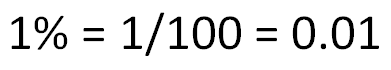
Основная связь между десятичными дробями и процентами

Чтобы преобразовать десятичную дробь в проценты, нам необходимо умножить на 100.

Например: 6 = 600%; 0,6 = 60%; 0,06 = 6%; 0,006 = 0,6%.

Чтобы преобразовать проценты в десятичную дробь, нам необходимо число процентов разделить на 100.

Например: 800% = 8; 80% = 0,8; 8% = 0,08; 0,8% — 0,008.

Как найти процент от числа?

Чтобы найти процент от числа, нужно:

1. Перевести % в десятичную дробь, это делается путем деления количества процентов на 100.
2. Полученную дробь необходимо умножить на известное число в задаче.

Задача 1

Пример задачи для решения:

Сплав содержит 10% меди. Сколько килограммов меди содержится в 650 килограммах сплава. Эта задача дана для нахождения процентов от числа, так как напротив 100% стоит число.

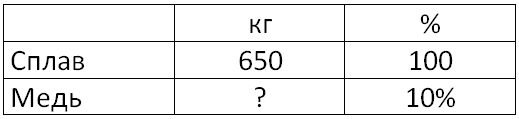
1. Нужно перевести: 10% = 0,1.

2. Решаем сколько кг меди содержится в 650 кг сплава: 0,1*650=65 кг.

Ответ: 65 кг.

Задача 2

Какую долю в процентном отношении составляет 25 от 500.

Формула в финансовых расчетах: P = A1 / A2 * 100%.

Решение: P = 25 / 500 * 100 = 5 %

Основные формулы для решения задач на проценты

• Формула вычисления процента от заданного числа

Если нам известно число А и нужно найти число В, тогда составляющее P процентов от A находится за формулой:

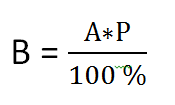
• Формула вычисления числа по его проценту

Если нам известно число В которое составляет P процентов от числа A, а также нужно найти значение числа A, это решается формулой:

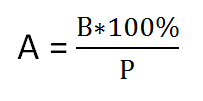
• Формула вычисления процентного выражение одного числа от другого

Если нам известно два числа А и В, а также нужно определить, какой процент составляет число В от числа А, то это находится за формулой:

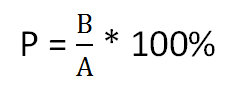
• Формула вычисления числа, которое больше исходного числа на заданный процент

Если нам известно число А и нужно найти число B, которое на P процентов больше числа A, то это находится за формулой:

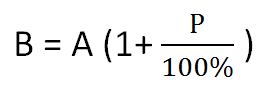
• Формула вычисления числа, которое меньше исходного числа на заданный процент

Если нам известно число А и нужно найти число B, которое на P процентов меньше числа A, то это находится за формулой:

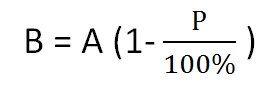
• Формула вычисления исходного числа по значению числа, которое больше от исходного на заданный процент

Если нам известно число В, которое на P процентов больше числа A, а также нужно найти число А, то это находится за формулой:

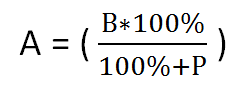
• Формула вычисления исходного числа по значению числа, которое меньше от исходного на заданный процент

Если нам известно число В, которое на P процентов меньше числа A, а также нужно найти число А, то это находится за формулой:

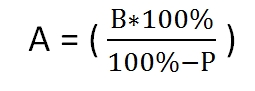
• Формула вычисления сложных процентов

Где в формуле А — это текущая стоимость, В — будущая стоимость, Р — процентная ставка за (день, месяц…), n — количество расчетных периодов.

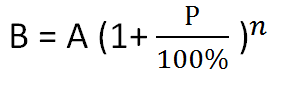
Решение задач на проценты — видео

pristor.ru

Вычисление процентов, или Повседневная математика :: SYL.ru

Вычисление процентов – несложная математическая операция, которая довольно часто встречается в повседневной жизни. Например, нужно посчитать, сколько человек экономит, используя дисконтную карту магазина или покупая товар на распродаже со скидкой, под какой процент берет кредит. Проценты можно посчитать при помощи калькулятора или пропорции, пригодится формула вычисления процентов и знание элементарных известных соотношений.

Что такое процент от числа

Вычисление процентов в школьной программе изучается классе в 5-м, если не раньше. Согласно определению, процент – это одна сотая часть числа. Термин появился в Древнем Риме и буквально переводится как «со ста». Первоначально идея вычислять проценты зародилась еще в Вавилоне. Параллельно в Древней Индии научились считать проценты при помощи пропорции.

Для того чтобы найти процент от числа, необходимо данное число поделить на 100. Очевидно, что 1 % от 100 равняется единице.

Вычисление процентов по формулам

Формула, позволяющая найти процент от числа, элементарна. Необходимо число поделить на 100, после чего умножить на нужный процент.

Если принять за Х исходное число, а за Y - искомый процент, то формула записывается в виде X/100*Y=...

Например, нужно рассчитать 25 % от числа 300. Расчет по вышеуказанной формуле будет иметь вид: 300/100*25=75.

Расчеты при помощи пропорции

Вычисление процентов можно производить, имея понимание метода пропорции. Пусть А - основное число, принятое за 100 %, В - число, соотношение которого с А в процентном соотношении необходимо высчитать, а Х - число искомых процентов. Тогда:

А - 100 %,В - Х %.

Умножение крест-накрест даст равенство: А*Х=В*100. Следовательно, Х=В*100/А.

Например, необходимо узнать, сколько процентов от 300 составляет число 75. Получается: 75*100/300=25 %.

Альтернативный метод вычислений

Представим один процент не десятичной, а простой дробью - 1/100. Аналогично можно записать любое количество процентов. Так, 10 % - это 0,1 или 1/10, 25 % - 0,25 или 25/100=1/4 и так далее. Следовательно, найти 10 % от числа довольно просто - нужно разделить исходное число на 10. Таким способом удобно вычислять 20, 25 и 50 процентов:

• 20 % - это 1/5, значит, нужно делить на 5 исходное число.
• 25 % - 1/4, нужно делить на 4.
• 50 % - это 1/2, просто делить на два.

Но не всякий процент удобно рассчитать таким методом. К примеру, 33 % - это 33/100, что при записи десятичной дробью дает 0,3333 с бесконечным количеством троек после запятой.

Если возникают сомнения в правильности проводимых расчетов, всегда можно проверить себя на калькуляторе, который сейчас есть в любом мобильном устройстве и на любом компьютере.

www.syl.ru

Проценты | Формулы с примерами

Правила нахождения процентов

Формула

Свойства

Свойство 1

Свойство

Нахождение p% от числа a: умножить a на	p	;
	100

Пример 4% от 190 равны 190 • 0,04 = 7,6;

23% от 53 равны 53 • 0,23 = 12,19;

131% от 19 равны 19 • 1,31 = 24,89;

Свойство 2

Свойство

Нахождение числа a, если его p% равны b: разделить b на	p	;
	100

Пример

Найти число, 16% которого равны 70: a =	70	=  437,5  =	1	;
	0,16		5

Найти число 175% которого равны 90: a =	90	= 51	1	;
	1,75		4

Найти число 250% которого равны 100: a =	100	=  0,4.
	2,5

Свойство 3

Свойство Выражение в процентах частного двух чисел a и b (дроби): Пример

15 : 20 =	15	• 100% = 75%.
	20

Свойство 4

Свойство Сколько процентов составляет число a от числа b: разделить a на b, полученную дробь записать в процентах: Пример Сколько процентов составляет число 30 от 60?

Процентное соотношение

Определение Процентное соотношение представляет какую-либо часть от единицыкак часть от 100. Обозначение процентов: %.

Обозначение 1% = 1/100, одна сотая часть величины.

100% - это единица, или некоторое количество целиком.

50% = 50/100, т.е. половина от целого.

formula-xyz.ru

Как посчитать проценты | Подскажем

Процент – сотая доля числа. Это математическое понятие широко применяется в повседневной жизни: в процентах указаны статистические данные, состав продуктов питания и различных материалов, а также ставки по кредитам и депозитам.

Проценты позволяют сравнивать между собой части целого, значительно упрощая расчеты Вычисление процентов можно выполнить в уме или на бумаге, используя формулу, а также с помощью калькулятора или программы Excel.

Быстрая навигация по статье

Расчет по формуле

Для того чтобы посчитать проценты при помощи формулы, необходимо:

• Число, от которого нужно найти процент, поделить на 100;
• Полученный результат умножить на искомый процент.

Для удобства число можно умножать на проценты, записанные в виде десятичной дроби (поделить их на сто). Например, чтобы найти 20% от 50, необходимо 50/100*20=10 или 50*0,2=10.

Вычисление на калькуляторе

Для подсчета процентов можно использовать калькулятор. Для этого потребуется:

• Ввести нужное число;
• Нажать кнопку «Умножить»;
• Указать количество процентов;
• Нажать клавишу «%».

Если обычного калькулятора нет в наличии, можно воспользоваться программой «Калькулятор» в операционной системе Windows (зайти в «Пуск», «Стандартные программы», «Калькулятор»). Существует также множество онлайн-калькуляторов, для использования которых необходим доступ к интернету.

Excel

Расчет процентов можно выполнять в программе Microsoft Office Excel. Для этого необходимо:

• Открыть программу;
• В любую ячейку ввести число, от которого нужно найти процент;
• В ячейку, в которой будет отображаться результат, поставить знак «=»;
• Выделить ячейку с указанным числом, ввести знак «*», ввести проценты, поставить значок «%» и нажать кнопку “Enter”;
• Во второй ячейке отобразится результат вычислений.

Вводить числа можно в любые ячейки файла (на одном листе или на разных).

Процентное соотношение

Существуют расчеты, позволяющие определить, сколько процентов составляет одно число от другого. Для такого расчета потребуется:

• Число, процентное соотношение которого нужно найти, необходимо умножить на 100;
• Результат поделить на число, от которого вычисляется процент.

Например, для того чтобы найти сколько процентов составляет 50 от 200, нужно 50*100/200=25 (50 составляет 25 процентов от 200).

Нахождение числа по проценту

Чтобы высчитать число по его проценту необходимо:

• Заданное число разделить на процент;
• Полученный результат умножить на 100.

Например, для нахождения числа, 25% от которого составляет 50, потребуется 50/25*100=200.

Поделитесь этой статьёй с друзьями в соц. сетях:

podskajem.com

Как посчитать (высчитать) процент от суммы?

Как посчитать процент от суммы, требуется знать во многих случаях (при расчете госпошлины, кредита и т. п.). Мы расскажем, как посчитать проценты от суммы с помощью калькулятора, пропорций и известных соотношений.

Как узнать процент от суммы в общем случае?

Как высчитать процент из суммы с помощью пропорции?

Как рассчитать процент от суммы с помощью известных соотношений?

Как вычесть процент от суммы без помощи калькулятора

Как высчитать (отнять) из суммы процент с калькулятором в руках

Как отнять от суммы процент с помощью онлайн-калькулятора

Как узнать процент от суммы в общем случае?

Перед тем как высчитать процент от суммы, необходимо рассчитать размер этого самого процента. Для этого достаточно взять общую сумму и разделить ее на 100 — результат будет составлять как раз 1%.

Читайте нас в Яндекс.Дзен

Яндекс.Дзен

После этого есть два варианта:

1. Если нужно узнать, сколько процентов составляет другая сумма от первоначальной, нужно просто разделить ее на размер 1%, полученный ранее.
2. Если же нужен размер суммы, которая составляет, скажем, 27,5% от первоначальной, нужно размер 1% умножить на требуемое количество процентов.

Как высчитать процент из суммы с помощью пропорции?

Но можно поступить и иначе. Для этого придется использовать знания о методе пропорций, который проходят в рамках школьного курса математики. Это будет выглядеть так.

Пусть у нас есть А — основная сумма, равная 100%, и В — сумма, соотношение которой с А в процентах нам нужно узнать. Записываем пропорцию:

А = 100

В = Х

(Х в данном случае — число процентов).

По правилам расчета пропорций мы получаем следующую формулу:

Х = 100 * В / А

Если же нужно узнать, сколько будет составлять сумма В при уже известном числе процентов от суммы А, формула будет выглядеть по-другому:

В = 100 * Х / А

Теперь остается подставить в формулу известные числа — и можно производить расчет.

Как рассчитать процент от суммы с помощью известных соотношений?

Наконец, можно воспользоваться и более простым способом. Для этого достаточно помнить, что 1% в виде десятичной дроби — это 0,01. Соответственно, 20% — это 0,2; 48% — 0,48; 37,5% — это 0,375 и т. д. Достаточно умножить исходную сумму на соответствующее число — и результат будет означать размер процентов.

Кроме того, иногда можно воспользоваться и простыми дробями. Например, 10% — это 0,1, то есть 1/10 следовательно, узнать, сколько составят 10%, просто: нужно всего лишь разделить исходную сумму на 10.

Другими примерами таких соотношений будут:

• 12,5% — 1/8, то есть нужно делить на 8;
• 20% — 1/5, то есть нужно разделить на 5;
• 25% — 1/4, то есть делим на 4;
• 50% — 1/2, то есть нужно разделить пополам;
• 75% — 3/4, то есть нужно разделить на 4 и умножить на 3.

Правда, не все простые дроби удобны для расчета процентов. К примеру, 1/3 близка по размерам к 33%, но не равна точно: 1/3 — это 33,(3)% (то есть дробь с бесконечными тройками после запятой).

Как вычесть процент от суммы без помощи калькулятора

Если же требуется от уже известной суммы отнять неизвестное число, составляющее какое-то количество процентов, можно воспользоваться следующими методами:

1. Вычислить неизвестное число с помощью одного из приведенных выше способов, после чего отнять его от исходного.
2. Сразу рассчитать остающуюся сумму. Для этого от 100% отнимаем то число процентов, которое нужно вычесть, и полученный результат переводим из процентов в число любым из описанных выше способов.

Второй пример удобнее, поэтому проиллюстрируем его. Допустим, надо узнать, сколько останется, если от 4779 отнять 16%. Расчет будет таким:

1. Отнимаем от 100 (общее количество процентов) 16. Получаем 84.
2. Считаем, сколько составит 84% от 4779. Получаем 4014,36.

Как высчитать (отнять) из суммы процент с калькулятором в руках

Все вышеприведенные вычисления проще делать, используя калькулятор. Он может быть как в виде отдельного устройства, так и в виде специальной программы на компьютере, смартфоне или обычном мобильнике (даже самые старые из ныне используемых устройств обычно имеют эту функцию). С их помощью вопрос, как высчитать процент из суммы, решается очень просто:

1. Набирается исходная сумма.
2. Нажимается знак «-».
3. Вводится число процентов, которое требуется вычесть.
4. Нажимается знак «%».
5. Нажимается знак «=».

В итоге на экране высвечивается искомое число.

Как отнять от суммы процент с помощью онлайн-калькулятора

Наконец, сейчас в сети достаточно сайтов, где реализована функция онлайн-калькулятора. В этом случае даже не требуется знания того, как посчитать процент от суммы: все операции пользователя сводятся к вводу в окошки нужных цифр (или передвижению ползунков для их получения), после чего результат сразу высвечивается на экране.

Особенно эта функция удобна тем, кто рассчитывает не просто абстрактный процент, а конкретный размер налогового вычета или сумму госпошлины. Дело в том, что в этом случае вычисления сложнее: требуется не только найти проценты, но и прибавить к ним постоянную часть суммы. Онлайн-калькулятор позволяет избежать подобных добавочных вычислений. Главное — выбрать сайт, пользующийся данными, которые соответствуют действующему закону.

nsovetnik.ru

Расчёт, формулы сложных процентов в Excel + калькулятор

Приветствую, читатели и посетители блога!

«Превратите 1$ в 1000000$!», «Самый простой способ стать миллионером!», «Вложи, ничего не делай и стань финансово свободным!». Вам попадались такие лозунги в Интернете? Мне да…

Впрочем, такие фразы возникли не на пустом месте. Любая статья, обучающий курс или другие материалы с таким заголовком – так или иначе, затрагивает тему сложного процента.

Вот и я вам предлагаю сегодня поговорить об этом удивительном инструменте богатства. Еще в самом начале ведения блога я затрагивал эту тему, когда искал ответ на вопрос – Зачем нужны инвестиции?.

Для начала, давайте разберемся кое в чём. Если есть сложный процент, есть и простой, не так ли? В чем разница?

И то, и другое — это способ начисления прибыли на депозиты и вложения. Но формулы сложных и простых процентов отличаются кардинально: в первом случае работает арифметическая прогрессия, во втором – геометрическая.

Если по-русски, то ключевое отличие двух процентов в том, что при простом проценте доход приносит только первоначальная сумма. Прибыль всегда будет одинаковой и через год, и через 10 лет.

Например, если инвестор получает 20% в год на 10000$ — это 2000$ в год. И каждый год сумма прибыли будет ровно 2000$.

С другой стороны, когда работает сложный процент, процент прибыли начисляется не только на первичную сумму инвестиций, но еще и на полученную прибыль. Это значит, что с каждым годом доход будет все выше и выше.

На тех же условиях, но с реинвестированием – в первый год инвестор получит 2000$, во второй – 2400$, в третий – 2880$. А через десять лет – 10320$! А через двадцать – невероятные 63896$. Что мы там говорили о том, как стать миллионером?

И это без учета дополнительных вложений.

Очень похоже на то, как катится с горы снежный ком – сначала понемногу, а со временем ком становится все больше и больше – и вот уже он огромен!

Для наглядности я сделал другой расчет сложных процентов в Excel и сравнил с простыми:

С каждым годом, с каждым месяцем разница все ощутимее и ощутимее

И чем дальше, тем сильнее заворачивается вверх красный график, устремляясь по параболе в финансовую бесконечность… Пусть и в теории, но зато как эффектно!

В принципе, особо тут разглагольствовать не о чем. В Интернет-инвестировании эффект сложного процента разрешен и чаще всего используется автоматически. Например, в ПАММ-счетах это так.

С другой стороны, инвесторам часто приходится рассчитывать сложный процент – подсчитать доходность, оценить инвестиционный горизонт… И решать другие прикладные задачи.

Поэтому дальше я покажу вам все необходимые формулы и помогу с расчетами.

Содержание:

Обзор задач и формул сложных процентов

Самая первая задача, с которой может столкнуться инвестор – «Сколько я получу денег, инвестируя»? Она решается, если известна начальная сумма и годовая процентная ставка доходности.

Для расчета используется формула сложных процентов с капитализацией:

Где:

• К0 — начальный капитал,
• К – результат инвестирования (финальный капитал)
• R – годовая процентная ставка
• m – период реинвестирования (в месяцах)
• n – количество периодов реинвестирования (месяцев, кварталов, лет)

Чтобы работать чисто с годовыми периодами, нужно убрать из знаменателя 12, а из числителя – m. Но я этого делать не буду, так как ПАММ-счета удобнее всего анализировать через среднемесячную доходность.

Давайте рассмотрим пару примеров.

Пример №1. Иван Иванов положил 7000$ на депозит в банке. Сейчас средняя ставка по долларовым депозитам в Украине – в районе 9% в год. Вклад будет переоформляться каждый год в течение 10 лет. Сколько в итоге будет денег на банковском счету?

К0 =7000$, R = 9% в год, m = 12 месяцев, n = 10 (10 периодов по 12 месяцев)

Капитал вырос почти в три раза, несмотря на мизерную доходность по депозитам.

Впрочем, деньги на ПАММ-счетах реинвестируются автоматически и постоянно. Кроме того, гарантий стабильного годового дохода нет…

Поэтому рекомендую для расчетов сложного процента в ПАММ-счетах использовать ежемесячный реинвест.

Пример №2. Пётр Петров вложил в ПАММ-счета 10000$. После анализа статистики выяснилось, что он может ожидать 30% чистой прибыли за год. И теперь Пётр хочет знать, каким будет размер капитала через полгода.

Вот, что получилось:

К0 =10000$, R = 30% в год, m = 1 месяц, n = 6 (6 периодов по 1 месяцу)

Для сравнения, без реинвестирования инвестор получил бы 11500$. То есть, на 97$ меньше, что почти не чувствуется – это всего лишь 0.97% от общего капитала.

Но давайте теперь посмотрим чуть дальше в следующем примере.

Пример №3. Исидор Сидоров вложил в ПАММ-счета 5000$. Он собирается активно управлять портфелем и рассчитывает на 50% в год в течение 5 лет. Какой капитал получится в итоге?

Для расчета снова используется формула сложных процентов. Только теперь периодов не 6, а 60 – в 5 годах 60 месяцев. Сколько же получилось?

К0 =5000$, R = 50% в год, m = 1 месяц, n = 60 (60 периодов по 1 месяцу)

Без реинвестирования прибыль составила бы 50%*5=250%. Соответственно, капитал бы вырос до 35000$. А с учетом сложного процента – на целых 106 тысяч! Теперь разница ощущается очень сильно.

И чем больше проходит времени, тем сильнее разница. Теоретически, вложив сегодня 1$ в банк, уже ваши правнуки стали бы миллионерами.

Я не раз видел, как эту «фишку» используют в фильмах. Например, сюжет может быть такой:

Когда-то давно кто-то спрятал честно или нечестно заработанные деньги в скромный банк. И забыл о деньгах. Или надолго попал в тюрьму. Или умер. В общем, о деньгах забыли.

И вот, через 20-30 лет этот счет обнаруживают, а там лежат миллионы или даже миллиарды долларов. И начинается охота за паролями, поиск владельца, взлом хитромудрых защитных систем и т.д. Что придумают сценаристы :)

В прошлой статье я упоминал о том, что консервативные ПАММ-счета растут по параболе из-за сложного процента. Теперь вы на 100% понимаете, как это работает!

Кроме постоянного реинвестирования прибыли, инвестор может дополнительно «доливать» деньги в свой портфель. Эти деньги тоже будут приносить доход, поэтому формула сложных процентов немного усложняется.

Ну как немного… В общем, смотрите:

AI (Additional Investments) – размер постоянного пополнения.

С левым слагаемым вы знакомы, а правое – расчет сложного процента по новым вложениям. Формула правильная, я проверял :)

------------ ↑ к содержанию ↑ ------------

Вспомогательные формул расчета сложных процентов

Из формулы, которую мы использовали раньше, можно получить несколько других, которые могут пригодиться инвестору при решении финансовых задач.

Например, иногда нужно найти не финальный, а начальный капитал.

Пример №4. Аркадий Аркадьев интересуется, сколько ему нужно вложить денег, чтобы получить через 5 лет при ставке доходности 30% в год 100000$. Реинвест – каждый квартал.

Для этого мы используем такую формулу:

Выглядит немного страшно, но цифры точно те же, что мы использовали до этого. Подставим наши данные в формулу и найдем начальный капитал:

K = 100000$, R = 30% в год, m = 3 месяца, n = 20 (5 лет – это 20 кварталов)

Оказалось, нужно почти в 5 раз меньше. Круто, не так ли?

Идем дальше. Давайте представим ситуацию – инвестор хочет вложить деньги на определенный срок. И он рассчитывает по итогам достичь определенной суммы капитала. Какую процентную ставку ему нужно получить?

Чтобы это узнать, для расчета нам нужна формула сложных процентов для средней процентной ставки:

Пример №5. Начальные инвестиции Максима Максимова – 13000$. Через два года они должны превратиться в 18000$. Реинвест ежемесячный (m= 1). Под какую ставку доходности Максиму нужно собирать инвестиционный портфель, чтобы выйти на требуемую сумму?

Подставляем числа:

K = 18000$, К0 =13000$, m = 1 месяц, n = 24 (2 года = 24 месяца)

Естественно, это годовая ставка. Её можно превратить в месячную, если из числителя убрать 12, и тогда получится около 1.5% в месяц – минимальный порог для ПАММ-счетов.

Что там можно еще найти? Ах, да – сколько нужно времени, чтобы получить определенную сумму при определенной ставке. Давайте попробуем :)

Если в прошлом примере у нас были корни, то теперь – логарифмы. Формулы кажутся огромными, но на самом деле их легко реализовать в программе. Чтобы рассчитать сложный процент, формула Excel нужна для одной ячейки – вот и выражаем одно через все остальное. И работает это отлично!

Итак, мы будем использовать такую формулу:

Пример №6. У Елены Лениной – 4500$, которые она хочет инвестировать. Она понимает, что может рассчитывать на 50% в год, при этом хочет достичь первой цели – 20000$. Возможно, хочет купить со временем новую машину :)

Через сколько времени она достигнет своей цели с условием ежемесячного реинвестирования прибыли? Подставляем числа:

K = 20000$, К0 =4500$, R = 50%, m = 1 месяц

Довольно быстро, должен сказать.

Кстати, опытных инвесторов часто интересует не на сколько, когда и как вырастет капитал. Их больше интересует, когда деньги удвоятся. Другими словами – через сколько они «отобьют» вложения.

Чтобы это узнать, существует универсальное «правило 72». Суть его простая – делите 72 на процентную ставку за месяц (квартал, год). Результат – это и есть тот срок, за который инвестиции удвоятся (в тех же единицах времени, что и ставка доходности).

Пример №7. Инвестор Владимир ВладимирОвич вкладывает деньги под 10% в месяц. Через сколько он отобьет вложения?

Ответ: через 72/10=7.2 месяца.

Вложения под 6% в месяц дают удвоение капитала за год. Под 3% — за 2 года.

------------ ↑ к содержанию ↑ ------------

Расчет сложных процентов в Excel по формулам

Многие из формул, которые я вам написал, на калькуляторе посчитать не то что неудобно – почти невозможно. Да и зачем это, если есть замечательная программа, о которой пишу чуть ли не в каждой статье :)

Например, в статье «Делаем собственный рейтинг ПАММ-счетов» я показал, как с помощью Excel проранжировать ПАММ-счета по нескольким показателям и автоматически найти самые выгодные варианты.

Поэтому я сделал для вас очередной полезный Excel-файлик – Калькулятор сложных процентов с капитализацией. Там вы найдете 5 табличек для расчетов по формулам из этой статьи.

Напоминаю, что мы искали:

• финальный капитал;
• финальный капитал с пополнениями;
• начальный капитал;
• процентную ставку;
• срок достижения инвестиционных целей.

В Калькуляторе сложных процентов эти задачи автоматизированы, используется формула сложных процентов в Excel (все виды), о которых мы говорили в этой статье. Надеюсь, пригодится :)

Скачать файл: «Расчет сложных процентов».

На всякий случай записал небольшую видеоинструкцию:

Если у вас нет Экселя или неудобно им пользоваться, можете попробовать поискать в Интернете сайты по запросам «калькулятор сложного процента с реинвестированием», «калькулятор сложного процента с капитализацией» или «калькулятор инвестора сложный процент». Вы найдете множество онлайн-сервисов, выбирайте, какой понравится.

------------ ↑ к содержанию ↑ ------------

И на этом я прощаюсь. По традиции, несколько вопросов к вам, читатели:)

Первое – как часто вам приходится считать сложный процент? И приходится ли? Лично мне не очень часто, но это потому что я считаю доходность ПАММ-счетов через интервалы – результат почти такой же выходит. Больше нигде применять не приходилось, кроме нескольких пар на втором курсе, когда мы учили «Финансовую математику».

Второе – есть ли у вас какие-то инвестиционные цели? Дойти до энной цифры с энным количеством нулей? Получить определенную доходность? Может, стать рантье? :)

Расскажите!

С уважением, Александр Дюбченко

Все статьи блога "Инвестируй в ЭТО"

Понравилась статья? Скажите "спасибо" лайком!

Нужно больше информации? Вот еще 4 статьи для вас:

investirui-v-eto.ru

Формула расчета процентов по кредиту и полной стоимости кредита

Многие граждане интересуются, какова формула расчета процентов по кредиту. Если смотреть статистические данные, то более 73% российских граждан в той или иной мере имели дело с кредитами: одни уже пользовались займами, а другие выплачивали принадлежащие не им долги.

В данной статье мы поможем разобраться с методикой расчета процентов по кредиту, а также расскажем, как производится расчет полной стоимости кредита, чтобы банковская организация не «заставила» вас платить больше, когда можно платить по более выгодной схеме.

Как произвести расчет процентов по кредиту?

Некоторые пользователи кредитных продуктов ошибочно предполагают, что посчитать проценты по кредиту самому сложно, но это не так. На самом деле, формула расчета процентов по кредиту напрямую связана с тем, какой вид платежа будет использован для погашения долга по кредиту:

• Дифференцированный платеж – ежемесячные выплаты по кредиту, размер которых уменьшается к даче окончания кредитного договора. В ежемесячный дифференцированный платеж входят сумма погашения тела кредита (основной долг) и проценты по кредиту, начисленные на оставшуюся сумму.
• Аннуитетный платеж – ежемесячные выплаты по кредиту, размер которых не меняется до окончания срока кредита. Но при аннуитетной схеме платежи вначале преимущественно идут в счет погашения процентов по кредиту, и в меньшей доле на тело кредита, и пропорция эта меняется уже ближе к концу кредитного договора.

Более наглядно отличия аннуитетных платежей от дифференцированных можно увидеть на вот этой схеме:

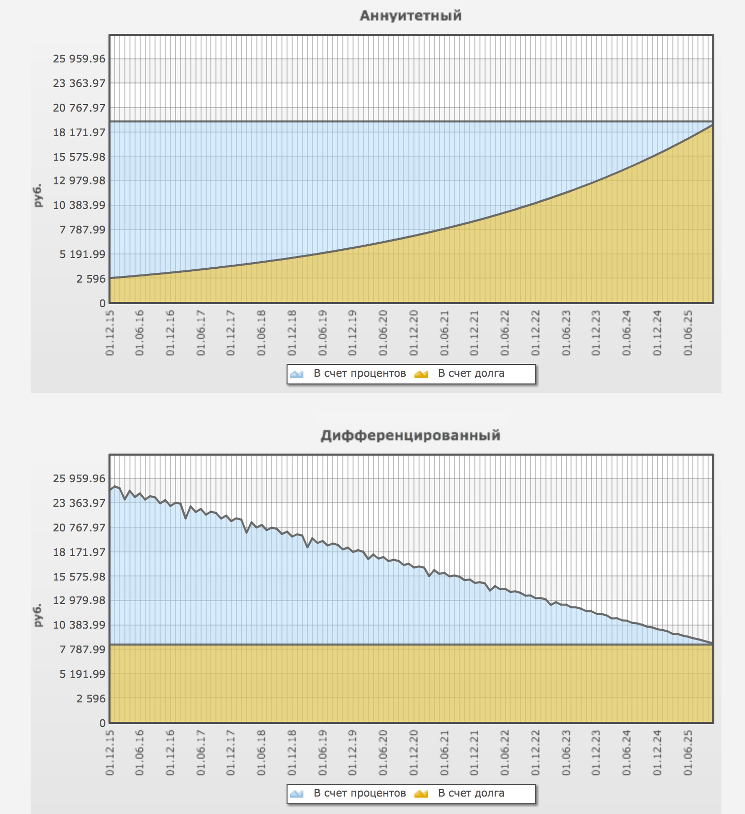
Банковские онлайн-калькуляторы расчета процентов по кредиту

Большинство граждан перед тем, как сделать выбор в сторону подходящего кредитного продукта, изучают информацию относительно условий кредитования и просчитывают проценты за пользование займом.

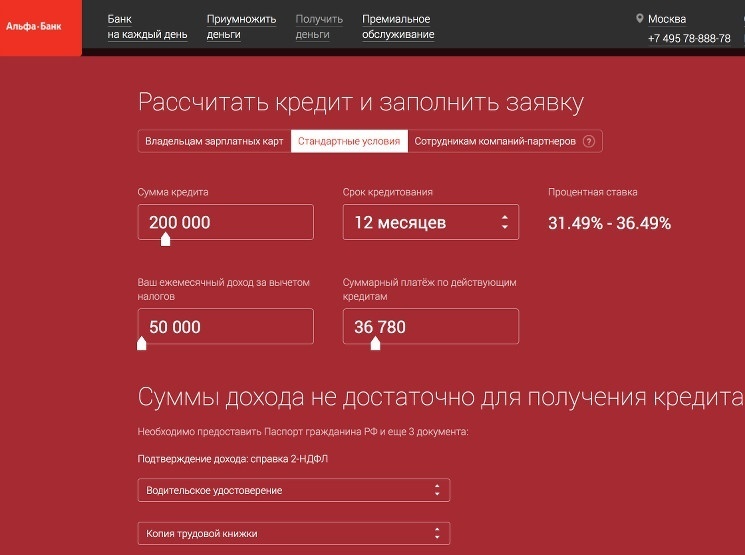
Сегодня на сайте многих банковских организаций есть специальный онлайн-сервис, представляющий собой кредитный калькулятор. Достаточно внести в графы необходимые вам условия кредитования и расчет будет произведен в считанные секунды. Кредитный калькулятор поможет определиться, какая сумма кредита в вашем случае будет самой оптимальной, если имеются какие-то сомнения. Вам необходимо ввести сумму своего дохода, ввести желаемый срок кредита и кликнуть на кнопку «Рассчитать».

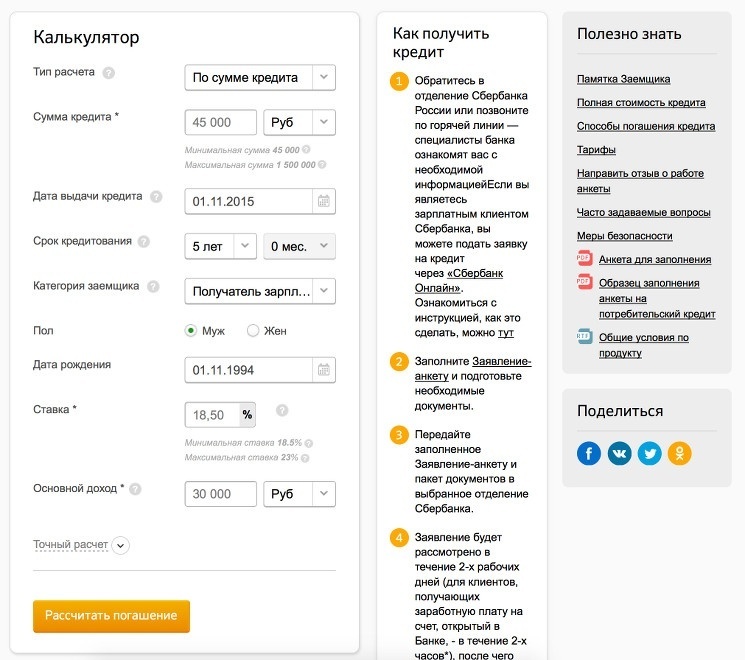
Таким образом, у потребителей есть возможность, не выходя из дома, не только выбрать кредитное учреждение, но и самый подходящий для его уровня доходов вид займа.

Формула расчета процентов по кредиту при дифференцированном платеже

Дифференцированный платеж, если углубляться в его суть, включает в себя две части:

• Тело кредита или основной долг;
• Проценты, начисленные на оставшуюся сумму основного долга.

Со временем сумма основного долга уменьшается, и по этой причине сумма процентов по кредиту, начисленных на эту сумму, тоже снижается. Существует простая формула, с помощью которой можно осуществить расчет суммы основного долга:

• ВД = ПСК/СК, где
• ВД – выплата основного долга;
• ПСК – первоначальная сумма кредита;
• СК – срок, который дан для возврата кредита.

Теперь рассчитаем проценты за пользование кредитом. Что касается расчетов процентов, то у каждого банка может быть своя позиция по данному вопросу, которая зависит от временного периода.

1. Первая позиция = 12 месяцев = 1 год. Здесь формула для расчета будет такая:

• СНП = ООД х ПГС / 12, где
• СНП – начисленные проценты по кредиту;
• ООД – остаток основного долга на момент расчета;
• ПГС – процентная годовая ставка.

2. Вторая позиция – 1 год = 365 дням. Формула расчета такова:

• СНП = ООД х ПГС х КДМ / 365
• СНП – сумма начисленных процентов;
• ООД – остаток основного долга на момент расчета;
• ПГС – годовая процентная ставка;
• КДМ – календарные дни в месяце. Это значение может быть от 28 до 31.

Формула расчета процентов по кредиту при аннуитетном платеже

Суть аннуитетного платежа состоит в том, что заемщик выплачивает его на протяжении всего срока займа без изменений установленной суммы. Бывают исключительные случаи, когда по договоренности между сторонами сумма кредита меняется. Аналогичная ситуация может произойти в случае досрочного погашения займа.

Аннуитетный платеж состоит из:

• Тела кредита (основного долга).
• Процентов по кредиту.

Формула для расчета аннуитетного платежа имеет следующий вид:

• РАП = ПСК*ПГС/1 – (1+ПГС) 1 – СК, где
• РАП – сумма платежа;
• ПСК – первоначальная сумма кредита;
• ПГС – годовая процентная ставка;
• СК – общий кредитный срок.

Это формула полной стоимости кредита в классическом исполнении, и именно ее придерживаются многие банковские организации. Эта формула является основой большинства кредитных калькуляторов.

Как рассчитывается ежемесячный платеж по кредиту?

Ежемесячно в определенный кредитным договором день заемщик обязан внести обязательный платеж за пользование кредитом. А знаете ли вы, из чего складывается данная сумма ежемесячного платежа по кредиту?

Вот составляющие платежа:

1. Сумма основного долга.
2. Страховой платеж.
3. Проценты, начисленные на тело кредита.
4. Всевозможные комиссионные сборы.

Большую часть платежа первоначально мы платим за пользование кредитом (проценты), но со временем эта составляющая становится меньше и идет погашение основного долга.

Относительно страховки в кредитной договоре вы должны знать: кредитные учреждения обязаны информировать заемщика перед заключением договора о том, что в контракте имеется пункт, где сказано, что он банк требует застраховать имущество, жизнь и здоровье заемщика, однако, это лишь требование банка, а не закона, поэтому заемщик вправе самостоятельно решать, хочет он покупать страховку при оформлении кредита или нет.

Заставлять заемщика принимать такие услуги никто не имеет право, так как пользователь кредитных ресурсов может выбрать другой банк или более приемлемый заем. В случае, когда банк не поставил клиента в известность о платежах в пользу страховых компаний, но в сумму ежемесячного взноса такая выплата была включена, заемщик имеет право обратиться в суд и обжаловать незаконные действия банка. Это возможно в том случае, если пункта о страховке нет в договоре.

Какой вид ежемесячных платежей по кредиту выбрать?

Мы уже говорили выше, что существует два вида кредитных платежей: дифференцированный и аннуитетный. Большинство заемщиков не имеют понятия, как эти платежи отличаются друг от друга, идут на поводу у банка, часто выбирая кредитный продукт, который для них не выгоден, а навязан банком. Стоит заострить внимание на этом моменте и разобраться в отличиях платежей.

Если смотреть с точки зрения выгоды, то банк отдает свой выбор в пользу аннуитетных платежей, так как они гарантируют переплату. А вот для заемщика выгодными являются дифференцированные платежи. Если смотреть детально, то при дифференцированных платежах в действительности сумма выплат со временем снижается. Но если сравнивать сумму первоначальных платежей, то становится видно, что если клиент выбрал дифференцированную систему платежей, то этот показатель будет выше. При аннуитетной системе суммы выплат со временем не меняются, и клиент погашает кредит равными суммами. По этой причине большинство банков выдвигает дополнительное условие для тех клиентов, которые желают воспользоваться дифференцированной системой платежа – более высокий уровень доходов, чем для тех, кто предпочел аннуитетную систему.

К середине срока выплаты кредита разница между указанными видами платежей уже станет заметной, так как основная составляющая платежа будет направлена на уплату процентов, а меньшая часть – на погашение основного тела кредита.

Многие заемщики предпочитают более понятную и «правильную» схему аннуитетных платежей по причине, что сумма ежемесячного платежа остается неизменной, поэтому дополнительно пересчитывать ничего не требуется, то есть банк не сможет никаким образом клиента обмануть.

Следует помнить, что перед подписанием кредитного договора, требуется внимательно прочитать все пункты документа особенно те, которые написаны мелким шрифтом. Даже учитывая тот факт, что борьба с мошенниками в лице сомнительных микрокредитных организаций, которые заставляют заемщиков платить баснословные проценты по кредитам, происходит на государственном уровне, довольно сложно оспорить договор, когда вы собственноручно поставили под ним подпись. Будьте внимательны, считайте свои деньги и вникайте в схемы кредита и условия платежей, требуйте раскрытия информации о полной стоимости кредита предлагаемого вам кредитной организацией.

www.papabankir.ru

---

• 
  Производство колбасы в домашних условиях как бизнес
• 
  Что такое воронка
• 
  Информационный повод
• 
  Нативная реклама это что
• 
  Выполнение плана
• 
  Холодный звонок пример диалога
• 
  Лучшие коммерческие предложения
• 
  Что такое кейс в бизнесе
• 
  Фандрайзер это
• 
  Что актуально сейчас
• 
  Би 2 би это